Slip (aerodynamics), Anterior chamber angle, Angle of the mandible

החלקה (אווירודינמיקה): החלקה היא מצב אווירודינמי שבו מטוס נע מעט לרוחב וגם קדימה יחסית לזרימת האוויר הקרובה או לרוח היחסית. במילים אחרות, עבור מטוס קונבנציונאלי, האף יפנה בכיוון ההפוך לגדת הכנף. המטוס לא נמצא בטיסה מתואמת ולכן הוא טס בצורה לא יעילה.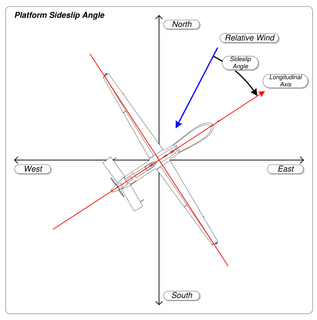
זווית תא קדמי: זווית החדר הקדמי היא חלק מהעין הנמצא בין הקרנית לאירוס המכיל את הרשת הטרבקולרית. גודל הזווית הזו הוא הקובע החשוב של קצב ההומור המימי שזורם מהעין, וכך, הלחץ התוך עיני. זווית החדר הקדמי היא המבנה הקובע את עומק החדר הקדמי. זווית תא קדמית צרה במיוחד היא תכונה של גלאוקומה של סגירת זווית.
זווית הלסת התחתונה: זווית הלסת התחתונה ממוקמת בגבול האחורי בצומת הגבול התחתון של ראמוס הלסת.
עֶצֶם הַשֶׁכֶם: באנטומיה, עצם השכמה , המכונה גם עצם הכתף , הכתף , עצם הכנף או עצם הלהב , היא העצם המחברת את עצם הזרוע עם עצם הבריח. כמו עצמותיהם המחוברות, עצמות השכמות מזווגות, כאשר כל עצם השכמה משני צידי הגוף מהווה בערך תמונת מראה של השנייה. השם נובע מהמילה הלטינית הקלאסית עבור כף או חפירה קטנה, שנחשבה דומה לה.
זווית חוט: זווית החוט של בורג היא הזווית הכלולה בין צלעות החוט, נמדדת במישור המכיל את ציר החוט. זהו גורם מגדיר לצורת הברגה. הערכים הסטנדרטיים כוללים:
גבול היציבות החיובית: גבול היציבות החיובית (LPS) או זווית היציבות הנעלמת (AVS) היא הזווית מהאנכי בו הסירה כבר לא תישאר זקופה אלא תתהפך, תהפוך או תתגרה.
זווית הראייה: זווית הראייה היא המשתנה הקובע לתפיסה החזותית של גודל או השלכה של גודל אובייקט.
בן לרנר: בנימין ס 'לרנר הוא משורר, סופר, מסאי ומבקר אמריקאי. הוא היה חוקר פולברייט, גמר בפרס פוליצר לסיפורת, גמר בפרס הספר הלאומי, גמר בפרס חוג מבקרי הספרים הלאומי, עמית קרן הווארד, עמית גוגנהיים ועמית מקארתור, בין היתר. הצטיינות. בשנת 2011 הוא זכה ב" Preis der Stadt Münster für internationale Poesie ", האמריקאי הראשון שזכה בכבוד. לרנר מלמד בקולג 'ברוקלין, שם התמנה לפרופסור מכובד לאנגלית בשנת 2016.
זווית היעד: זווית היעד היא הנושא היחסי של תחנת התצפית מהרכב הנצפה. ניתן להשתמש בו לצורך חישוב נקודת הכוונה לבעיית בקרת אש כאשר ניתן לאמוד את טווח ומהירות הרכב מתוך מידע אחר. ניתן להסביר את זווית היעד בצורה הטובה ביותר מהדוגמה של צוללת המתכוננת לשגר טורפדו ישר (לא ביתי) לעבר ספינת יעד נעה. מכיוון שהטורפדו נע לאט יחסית, יש לכוון את מסלול הטורפדו לא לכיוון המטרה, אלא לכיוון היכן המטרה תהיה כשהטורפדו מגיע אליו. זווית היעד משמשת להערכת מהלך היעד.
צלחת זווית: לוח זווית הוא מכשיר להחזקת עבודה המשמש כמתקן בעיבוד מתכות.
מנורת Anglepoise: מנורת Anglepoise היא מנורה מאוזנת שעוצבה בשנת 1932 על ידי המעצב הבריטי ג'ורג 'קרוורדין.
פוסט (מבני): עמוד הוא תומך אנכי או נוטה במבנה הדומה לעמוד או לעמוד, אך המונח עמוד מתייחס בדרך כלל לעץ אך עשוי להיות מתכת או אבן. חתיכה בבניית בניין מעץ או מתכת דומה אך חובה קלה יותר ממוט ויתד עשוי להיות דומה לחתיכה או לשמש סוגר. בבריטניה יתד עשוי להיות דומה מאוד למוצב אך אינו נושא קרן. בעמדות בניית עץ נוחתות בדרך כלל על אדן אדמה, אך בסוגים נדירים של בניינים העמוד עשוי להמשיך עד ליסוד המכונה אדן קטוע או לקרקע הנקראת אדמה, בנייה באדמה או לאחר חור. מוצב הוא גם יסוד מהותי בגדר. המונחים "ג'ק" ו"נכה "משמשים עם חתיכים וקורות מקוצרים, אך לא עם מוטות, למעט אוצר המילים המיוחד של shoring.
משולש: משולש הוא מצולע עם שלושה קצוות ושלושה קודקודים. זו אחת הצורות הבסיסיות בגיאומטריה. משולש עם קודקודים A , B ו- C מסומן .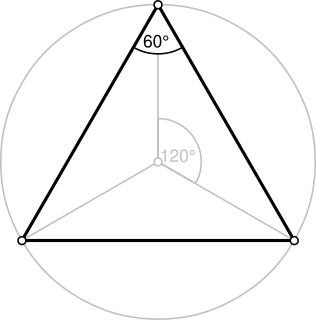
גילמט: גילימטים הם צמד סימני פיסוק בצורת שברונים כפולים לרוחב, « ו- » , המשמשים כמרכאות במספר שפות. בחלק מהשפות הללו משתמשים ב"גילמט "בודדים, ‹ ו › עבור הצעת מחיר בתוך ציטוט אחר. Guillemets אינם משמשים באופן מקובל בשפה האנגלית.
מרכאות: מרכאות , המוכרות גם כמרכאות , מרכאות , סימני דיבור , פסיקים הפוכים או סימני דיבור , הן סימני פיסוק המשמשים בזוגות במערכות כתיבה שונות בכדי להפחית דיבור ישיר, ציטוט או ביטוי. הצמד מורכב ממרכאות פתיחה וסימן מרכאות, שיכול להיות או לא יכול להיות אותו תו.
קוֹרָה: מסתנן הוא אחד מסדרה של חברים מבניים משופעים כגון קורות עץ שמרחיבים מהרכס או ירך אל צלחת הקיר, במדרון היקפי או המדף, וכי נועדו לתמוך רעפי גגות, סיפון הגג המון קשור אליו. זוג קורות קוראים זוג . בבנייה ביתית, קורות עץ עשויות בדרך כלל מעץ. קורות חשופות הן תכונה של כמה סגנונות גג מסורתיים.
בַּרקִית: גלאוקומה היא קבוצה של מחלות עיניים אשר גורמות לפגיעה בעצב הראייה וגורמות לאובדן ראייה. הסוג הנפוץ ביותר הוא גלאוקומה בזווית פתוחה , בה זווית הניקוז של נוזלים בעין נותרת פתוחה, עם סוגים פחות נפוצים כולל גלאוקומה בזווית סגורה וגלאוקומה במתח רגיל. גלאוקומה בזווית פתוחה מתפתחת באטיות לאורך זמן ואין כאב. הראייה ההיקפית עשויה להתחיל לרדת, ואחריה הראייה המרכזית, וכתוצאה מכך עיוורון אם אינו מטופל. גלאוקומה של זווית סגורה יכולה להופיע בהדרגה או בפתאומיות. המצגת הפתאומית עשויה להיות כרוכה בכאבי עיניים חזקים, ראייה מטושטשת, אישון באמצע הרחבה, אדמומיות בעין ובחילה. אובדן הראייה מגלאוקומה, לאחר שהתרחש, הוא קבוע. עיניים המושפעות מגלאוקומה מכונות גלאוקומטיות .
ספקטרוסקופיית פוטו-פליטה עם זווית נפתרת: ספקטרוסקופיית פוטו-פליטה עם זווית ( ARPES ) היא טכניקה ניסיונית המשמשת בפיזיקה של חומר מעובה כדי לחקור את האנרגיות והמומנטה המותרים של האלקטרונים בחומר, בדרך כלל מוצק גבישי. הוא מבוסס על האפקט הפוטואלקטרי, שבו פוטון נכנס של אנרגיה מספקת פולט אלקטרון מפני השטח של חומר. על ידי מדידה ישירה של האנרגיה הקינטית והתפלגויות זווית הפליטה של ​​הפוטואלקטרונים הנפלטים, הטכניקה יכולה למפות את מבנה הלהקה האלקטרונית ומשטחי פרמי. ARPES הוא המתאים ביותר לחקר חומרים חד-ממדיים או דו-ממדיים. הוא שימש את הפיזיקאים לחקר מוליכי-על בטמפרטורה גבוהה, גרפן, חומרים טופולוגיים, מצבי בארות קוונטיות וחומרים המציגים גלי צפיפות מטען.
דיסק חיתוך: מטחנת זווית , המכונה גם מטחנת צד או מטחנת דיסק , היא כלי חשמל כף יד המשמש לטחינה ולליטוש. למרות שפותח במקור ככלי לדיסקים שוחקים קשיחים, הזמינות של מקור כוח מתחלף עודדה את השימוש בהם עם מגוון רחב של חותכים ותוספים.
בית הספר לזווית ליישור שיניים: בית הספר לזווית ליישור שיניים היה בית הספר הראשון ליישור שיניים בעולם, שהוקם על ידי אדוארד אנגל בשנת 1899. בית הספר לימד את תלמידיו יישור שיניים במשך תקופה של 3–6 שבועות. בית הספר סיים 183 סטודנטים עד לסגירתו בשנת 1927. בקרב הבוגרים הפכו 25 סטודנטים לנשיאי האיגוד האמריקני לאורתודונטים, 11 סטודנטים הפכו לראש המחלקות ליישור שיניים ושלושה סטודנטים הפכו לדיקני בית הספר לרפואת שיניים.
שסתום בוכנה במושב זוויתי: שסתום בוכנה למושב זוויתי הוא שסתום הנשלט באמצעות פנאומט עם מפעיל בוכנה המספק הפעלה לינארית להעלאת אטם ממושבו. המושב מוגדר בזווית כדי לספק את הזרימה המרבית האפשרית כאשר לא יושב. שסתומי בוכנה של מושב זוויתי מתאימים במיוחד ליישומים בהם נדרשים טמפרטורות גבוהות ושיעורי זרימה גדולים, כגון קיטור או מים. כאשר משתמשים בהם לאחור, ישנם דגמים של שסתום בוכנה במושב זוויתי שיחסלו את פטיש המים בעת הפעלתו.
גווני זווית: גווני הזווית הם עש של בני המשפחה Noctuidae. המין תואר לראשונה על ידי קרל לינאוס במהדורתו העשירית של Systema Naturae משנת 1758. הוא מופץ ברחבי אירופה עד מזרח האוראל וגם באיים האזוריים, באלג'יריה ובאסיה הקטנה, ארמניה וסוריה. זה נודד מאוד.
בגידות בפוקר: רמאות בפוקר היא כל התנהגות שמחוץ לחוקים שנועדה לתת יתרון לא הוגן לשחקן אחד או יותר.
זן טבעת: בכימיה אורגנית, זן הטבעת הוא סוג של חוסר יציבות שקיים כאשר קשרים במולקולה יוצרים זוויות לא תקינות. זן נדון לרוב עבור טבעות קטנות כגון cyclopropanes ו cyclobutanes, שזוויותיהם הפנימיות קטנות משמעותית מהערך האידיאלי של 109 ° בערך. בגלל המתח הגבוה שלהם, חום הבעירה של הטבעות הקטנות הללו מוגבה.
רשימת זהויות טריגונומטריות: במתמטיקה, זהויות טריגונומטריות הן שוויוניות הכוללות פונקציות טריגונומטריות ונכונות לכל ערך של המשתנים המתרחשים עבורם מוגדרים שני הצדדים של השוויון. מבחינה גיאומטרית, מדובר בזהויות הכוללות פונקציות מסוימות של זווית אחת או יותר. הם נבדלים מזהות משולש, שהם זהויות שעלולות להיות כרוכות בזוויות, אך כוללות גם אורכי צד או אורכים אחרים של משולש.
רשימת זהויות טריגונומטריות: במתמטיקה, זהויות טריגונומטריות הן שוויוניות הכוללות פונקציות טריגונומטריות ונכונות לכל ערך של המשתנים המתרחשים עבורם מוגדרים שני הצדדים של השוויון. מבחינה גיאומטרית, מדובר בזהויות הכוללות פונקציות מסוימות של זווית אחת או יותר. הם נבדלים מזהות משולש, שהם זהויות שעלולות להיות כרוכות בזוויות, אך כוללות גם אורכי צד או אורכים אחרים של משולש.
רשימת זהויות טריגונומטריות: במתמטיקה, זהויות טריגונומטריות הן שוויוניות הכוללות פונקציות טריגונומטריות ונכונות לכל ערך של המשתנים המתרחשים עבורם מוגדרים שני הצדדים של השוויון. מבחינה גיאומטרית, מדובר בזהויות הכוללות פונקציות מסוימות של זווית אחת או יותר. הם נבדלים מזהות משולש, שהם זהויות שעלולות להיות כרוכות בזוויות, אך כוללות גם אורכי צד או אורכים אחרים של משולש.
רשימת זהויות טריגונומטריות: במתמטיקה, זהויות טריגונומטריות הן שוויוניות הכוללות פונקציות טריגונומטריות ונכונות לכל ערך של המשתנים המתרחשים עבורם מוגדרים שני הצדדים של השוויון. מבחינה גיאומטרית, מדובר בזהויות הכוללות פונקציות מסוימות של זווית אחת או יותר. הם נבדלים מזהות משולש, שהם זהויות שעלולות להיות כרוכות בזוויות, אך כוללות גם אורכי צד או אורכים אחרים של משולש.
רשימת זהויות טריגונומטריות: במתמטיקה, זהויות טריגונומטריות הן שוויוניות הכוללות פונקציות טריגונומטריות ונכונות לכל ערך של המשתנים המתרחשים עבורם מוגדרים שני הצדדים של השוויון. מבחינה גיאומטרית, מדובר בזהויות הכוללות פונקציות מסוימות של זווית אחת או יותר. הם נבדלים מזהות משולש, שהם זהויות שעלולות להיות כרוכות בזוויות, אך כוללות גם אורכי צד או אורכים אחרים של משולש.
רשימת זהויות טריגונומטריות: במתמטיקה, זהויות טריגונומטריות הן שוויוניות הכוללות פונקציות טריגונומטריות ונכונות לכל ערך של המשתנים המתרחשים עבורם מוגדרים שני הצדדים של השוויון. מבחינה גיאומטרית, מדובר בזהויות הכוללות פונקציות מסוימות של זווית אחת או יותר. הם נבדלים מזהות משולש, שהם זהויות שעלולות להיות כרוכות בזוויות, אך כוללות גם אורכי צד או אורכים אחרים של משולש.
רשימת זהויות טריגונומטריות: במתמטיקה, זהויות טריגונומטריות הן שוויוניות הכוללות פונקציות טריגונומטריות ונכונות לכל ערך של המשתנים המתרחשים עבורם מוגדרים שני הצדדים של השוויון. מבחינה גיאומטרית, מדובר בזהויות הכוללות פונקציות מסוימות של זווית אחת או יותר. הם נבדלים מזהות משולש, שהם זהויות שעלולות להיות כרוכות בזוויות, אך כוללות גם אורכי צד או אורכים אחרים של משולש.
רשימת זהויות טריגונומטריות: במתמטיקה, זהויות טריגונומטריות הן שוויוניות הכוללות פונקציות טריגונומטריות ונכונות לכל ערך של המשתנים המתרחשים עבורם מוגדרים שני הצדדים של השוויון. מבחינה גיאומטרית, מדובר בזהויות הכוללות פונקציות מסוימות של זווית אחת או יותר. הם נבדלים מזהות משולש, שהם זהויות שעלולות להיות כרוכות בזוויות, אך כוללות גם אורכי צד או אורכים אחרים של משולש.
רשימת זהויות טריגונומטריות: במתמטיקה, זהויות טריגונומטריות הן שוויוניות הכוללות פונקציות טריגונומטריות ונכונות לכל ערך של המשתנים המתרחשים עבורם מוגדרים שני הצדדים של השוויון. מבחינה גיאומטרית, מדובר בזהויות הכוללות פונקציות מסוימות של זווית אחת או יותר. הם נבדלים מזהות משולש, שהם זהויות שעלולות להיות כרוכות בזוויות, אך כוללות גם אורכי צד או אורכים אחרים של משולש.
רשימת זהויות טריגונומטריות: במתמטיקה, זהויות טריגונומטריות הן שוויוניות הכוללות פונקציות טריגונומטריות ונכונות לכל ערך של המשתנים המתרחשים עבורם מוגדרים שני הצדדים של השוויון. מבחינה גיאומטרית, מדובר בזהויות הכוללות פונקציות מסוימות של זווית אחת או יותר. הם נבדלים מזהות משולש, שהם זהויות שעלולות להיות כרוכות בזוויות, אך כוללות גם אורכי צד או אורכים אחרים של משולש.
רשימת זהויות טריגונומטריות: במתמטיקה, זהויות טריגונומטריות הן שוויוניות הכוללות פונקציות טריגונומטריות ונכונות לכל ערך של המשתנים המתרחשים עבורם מוגדרים שני הצדדים של השוויון. מבחינה גיאומטרית, מדובר בזהויות הכוללות פונקציות מסוימות של זווית אחת או יותר. הם נבדלים מזהות משולש, שהם זהויות שעלולות להיות כרוכות בזוויות, אך כוללות גם אורכי צד או אורכים אחרים של משולש.
רשימת זהויות טריגונומטריות: במתמטיקה, זהויות טריגונומטריות הן שוויוניות הכוללות פונקציות טריגונומטריות ונכונות לכל ערך של המשתנים המתרחשים עבורם מוגדרים שני הצדדים של השוויון. מבחינה גיאומטרית, מדובר בזהויות הכוללות פונקציות מסוימות של זווית אחת או יותר. הם נבדלים מזהות משולש, שהם זהויות שעלולות להיות כרוכות בזוויות, אך כוללות גם אורכי צד או אורכים אחרים של משולש.
רשימת זהויות טריגונומטריות: במתמטיקה, זהויות טריגונומטריות הן שוויוניות הכוללות פונקציות טריגונומטריות ונכונות לכל ערך של המשתנים המתרחשים עבורם מוגדרים שני הצדדים של השוויון. מבחינה גיאומטרית, מדובר בזהויות הכוללות פונקציות מסוימות של זווית אחת או יותר. הם נבדלים מזהות משולש, שהם זהויות שעלולות להיות כרוכות בזוויות, אך כוללות גם אורכי צד או אורכים אחרים של משולש.
רשימת זהויות טריגונומטריות: במתמטיקה, זהויות טריגונומטריות הן שוויוניות הכוללות פונקציות טריגונומטריות ונכונות לכל ערך של המשתנים המתרחשים עבורם מוגדרים שני הצדדים של השוויון. מבחינה גיאומטרית, מדובר בזהויות הכוללות פונקציות מסוימות של זווית אחת או יותר. הם נבדלים מזהות משולש, שהם זהויות שעלולות להיות כרוכות בזוויות, אך כוללות גם אורכי צד או אורכים אחרים של משולש.
רשימת זהויות טריגונומטריות: במתמטיקה, זהויות טריגונומטריות הן שוויוניות הכוללות פונקציות טריגונומטריות ונכונות לכל ערך של המשתנים המתרחשים עבורם מוגדרים שני הצדדים של השוויון. מבחינה גיאומטרית, מדובר בזהויות הכוללות פונקציות מסוימות של זווית אחת או יותר. הם נבדלים מזהות משולש, שהם זהויות שעלולות להיות כרוכות בזוויות, אך כוללות גם אורכי צד או אורכים אחרים של משולש.
רשימת זהויות טריגונומטריות: במתמטיקה, זהויות טריגונומטריות הן שוויוניות הכוללות פונקציות טריגונומטריות ונכונות לכל ערך של המשתנים המתרחשים עבורם מוגדרים שני הצדדים של השוויון. מבחינה גיאומטרית, מדובר בזהויות הכוללות פונקציות מסוימות של זווית אחת או יותר. הם נבדלים מזהות משולש, שהם זהויות שעלולות להיות כרוכות בזוויות, אך כוללות גם אורכי צד או אורכים אחרים של משולש.
רשימת זהויות טריגונומטריות: במתמטיקה, זהויות טריגונומטריות הן שוויוניות הכוללות פונקציות טריגונומטריות ונכונות לכל ערך של המשתנים המתרחשים עבורם מוגדרים שני הצדדים של השוויון. מבחינה גיאומטרית, מדובר בזהויות הכוללות פונקציות מסוימות של זווית אחת או יותר. הם נבדלים מזהות משולש, שהם זהויות שעלולות להיות כרוכות בזוויות, אך כוללות גם אורכי צד או אורכים אחרים של משולש.
רשימת זהויות טריגונומטריות: במתמטיקה, זהויות טריגונומטריות הן שוויוניות הכוללות פונקציות טריגונומטריות ונכונות לכל ערך של המשתנים המתרחשים עבורם מוגדרים שני הצדדים של השוויון. מבחינה גיאומטרית, מדובר בזהויות הכוללות פונקציות מסוימות של זווית אחת או יותר. הם נבדלים מזהות משולש, שהם זהויות שעלולות להיות כרוכות בזוויות, אך כוללות גם אורכי צד או אורכים אחרים של משולש.
רשימת זהויות טריגונומטריות: במתמטיקה, זהויות טריגונומטריות הן שוויוניות הכוללות פונקציות טריגונומטריות ונכונות לכל ערך של המשתנים המתרחשים עבורם מוגדרים שני הצדדים של השוויון. מבחינה גיאומטרית, מדובר בזהויות הכוללות פונקציות מסוימות של זווית אחת או יותר. הם נבדלים מזהות משולש, שהם זהויות שעלולות להיות כרוכות בזוויות, אך כוללות גם אורכי צד או אורכים אחרים של משולש.
רשימת זהויות טריגונומטריות: במתמטיקה, זהויות טריגונומטריות הן שוויוניות הכוללות פונקציות טריגונומטריות ונכונות לכל ערך של המשתנים המתרחשים עבורם מוגדרים שני הצדדים של השוויון. מבחינה גיאומטרית, מדובר בזהויות הכוללות פונקציות מסוימות של זווית אחת או יותר. הם נבדלים מזהות משולש, שהם זהויות שעלולות להיות כרוכות בזוויות, אך כוללות גם אורכי צד או אורכים אחרים של משולש.
רשימת זהויות טריגונומטריות: במתמטיקה, זהויות טריגונומטריות הן שוויוניות הכוללות פונקציות טריגונומטריות ונכונות לכל ערך של המשתנים המתרחשים עבורם מוגדרים שני הצדדים של השוויון. מבחינה גיאומטרית, מדובר בזהויות הכוללות פונקציות מסוימות של זווית אחת או יותר. הם נבדלים מזהות משולש, שהם זהויות שעלולות להיות כרוכות בזוויות, אך כוללות גם אורכי צד או אורכים אחרים של משולש.
רשימת זהויות טריגונומטריות: במתמטיקה, זהויות טריגונומטריות הן שוויוניות הכוללות פונקציות טריגונומטריות ונכונות לכל ערך של המשתנים המתרחשים עבורם מוגדרים שני הצדדים של השוויון. מבחינה גיאומטרית, מדובר בזהויות הכוללות פונקציות מסוימות של זווית אחת או יותר. הם נבדלים מזהות משולש, שהם זהויות שעלולות להיות כרוכות בזוויות, אך כוללות גם אורכי צד או אורכים אחרים של משולש.
רשימת זהויות טריגונומטריות: במתמטיקה, זהויות טריגונומטריות הן שוויוניות הכוללות פונקציות טריגונומטריות ונכונות לכל ערך של המשתנים המתרחשים עבורם מוגדרים שני הצדדים של השוויון. מבחינה גיאומטרית, מדובר בזהויות הכוללות פונקציות מסוימות של זווית אחת או יותר. הם נבדלים מזהות משולש, שהם זהויות שעלולות להיות כרוכות בזוויות, אך כוללות גם אורכי צד או אורכים אחרים של משולש.
רשימת זהויות טריגונומטריות: במתמטיקה, זהויות טריגונומטריות הן שוויוניות הכוללות פונקציות טריגונומטריות ונכונות לכל ערך של המשתנים המתרחשים עבורם מוגדרים שני הצדדים של השוויון. מבחינה גיאומטרית, מדובר בזהויות הכוללות פונקציות מסוימות של זווית אחת או יותר. הם נבדלים מזהות משולש, שהם זהויות שעלולות להיות כרוכות בזוויות, אך כוללות גם אורכי צד או אורכים אחרים של משולש.
רשימת זהויות טריגונומטריות: במתמטיקה, זהויות טריגונומטריות הן שוויוניות הכוללות פונקציות טריגונומטריות ונכונות לכל ערך של המשתנים המתרחשים עבורם מוגדרים שני הצדדים של השוויון. מבחינה גיאומטרית, מדובר בזהויות הכוללות פונקציות מסוימות של זווית אחת או יותר. הם נבדלים מזהות משולש, שהם זהויות שעלולות להיות כרוכות בזוויות, אך כוללות גם אורכי צד או אורכים אחרים של משולש.
רשימת זהויות טריגונומטריות: במתמטיקה, זהויות טריגונומטריות הן שוויוניות הכוללות פונקציות טריגונומטריות ונכונות לכל ערך של המשתנים המתרחשים עבורם מוגדרים שני הצדדים של השוויון. מבחינה גיאומטרית, מדובר בזהויות הכוללות פונקציות מסוימות של זווית אחת או יותר. הם נבדלים מזהות משולש, שהם זהויות שעלולות להיות כרוכות בזוויות, אך כוללות גם אורכי צד או אורכים אחרים של משולש.
רשימת זהויות טריגונומטריות: במתמטיקה, זהויות טריגונומטריות הן שוויוניות הכוללות פונקציות טריגונומטריות ונכונות לכל ערך של המשתנים המתרחשים עבורם מוגדרים שני הצדדים של השוויון. מבחינה גיאומטרית, מדובר בזהויות הכוללות פונקציות מסוימות של זווית אחת או יותר. הם נבדלים מזהות משולש, שהם זהויות שעלולות להיות כרוכות בזוויות, אך כוללות גם אורכי צד או אורכים אחרים של משולש.
רשימת זהויות טריגונומטריות: במתמטיקה, זהויות טריגונומטריות הן שוויוניות הכוללות פונקציות טריגונומטריות ונכונות לכל ערך של המשתנים המתרחשים עבורם מוגדרים שני הצדדים של השוויון. מבחינה גיאומטרית, מדובר בזהויות הכוללות פונקציות מסוימות של זווית אחת או יותר. הם נבדלים מזהות משולש, שהם זהויות שעלולות להיות כרוכות בזוויות, אך כוללות גם אורכי צד או אורכים אחרים של משולש.
רשימת זהויות טריגונומטריות: במתמטיקה, זהויות טריגונומטריות הן שוויוניות הכוללות פונקציות טריגונומטריות ונכונות לכל ערך של המשתנים המתרחשים עבורם מוגדרים שני הצדדים של השוויון. מבחינה גיאומטרית, מדובר בזהויות הכוללות פונקציות מסוימות של זווית אחת או יותר. הם נבדלים מזהות משולש, שהם זהויות שעלולות להיות כרוכות בזוויות, אך כוללות גם אורכי צד או אורכים אחרים של משולש.
רשימת זהויות טריגונומטריות: במתמטיקה, זהויות טריגונומטריות הן שוויוניות הכוללות פונקציות טריגונומטריות ונכונות לכל ערך של המשתנים המתרחשים עבורם מוגדרים שני הצדדים של השוויון. מבחינה גיאומטרית, מדובר בזהויות הכוללות פונקציות מסוימות של זווית אחת או יותר. הם נבדלים מזהות משולש, שהם זהויות שעלולות להיות כרוכות בזוויות, אך כוללות גם אורכי צד או אורכים אחרים של משולש.
רשימת זהויות טריגונומטריות: במתמטיקה, זהויות טריגונומטריות הן שוויוניות הכוללות פונקציות טריגונומטריות ונכונות לכל ערך של המשתנים המתרחשים עבורם מוגדרים שני הצדדים של השוויון. מבחינה גיאומטרית, מדובר בזהויות הכוללות פונקציות מסוימות של זווית אחת או יותר. הם נבדלים מזהות משולש, שהם זהויות שעלולות להיות כרוכות בזוויות, אך כוללות גם אורכי צד או אורכים אחרים של משולש.
רשימת זהויות טריגונומטריות: במתמטיקה, זהויות טריגונומטריות הן שוויוניות הכוללות פונקציות טריגונומטריות ונכונות לכל ערך של המשתנים המתרחשים עבורם מוגדרים שני הצדדים של השוויון. מבחינה גיאומטרית, מדובר בזהויות הכוללות פונקציות מסוימות של זווית אחת או יותר. הם נבדלים מזהות משולש, שהם זהויות שעלולות להיות כרוכות בזוויות, אך כוללות גם אורכי צד או אורכים אחרים של משולש.
רשימת זהויות טריגונומטריות: במתמטיקה, זהויות טריגונומטריות הן שוויוניות הכוללות פונקציות טריגונומטריות ונכונות לכל ערך של המשתנים המתרחשים עבורם מוגדרים שני הצדדים של השוויון. מבחינה גיאומטרית, מדובר בזהויות הכוללות פונקציות מסוימות של זווית אחת או יותר. הם נבדלים מזהות משולש, שהם זהויות שעלולות להיות כרוכות בזוויות, אך כוללות גם אורכי צד או אורכים אחרים של משולש.
רשימת זהויות טריגונומטריות: במתמטיקה, זהויות טריגונומטריות הן שוויוניות הכוללות פונקציות טריגונומטריות ונכונות לכל ערך של המשתנים המתרחשים עבורם מוגדרים שני הצדדים של השוויון. מבחינה גיאומטרית, מדובר בזהויות הכוללות פונקציות מסוימות של זווית אחת או יותר. הם נבדלים מזהות משולש, שהם זהויות שעלולות להיות כרוכות בזוויות, אך כוללות גם אורכי צד או אורכים אחרים של משולש.
רשימת זהויות טריגונומטריות: במתמטיקה, זהויות טריגונומטריות הן שוויוניות הכוללות פונקציות טריגונומטריות ונכונות לכל ערך של המשתנים המתרחשים עבורם מוגדרים שני הצדדים של השוויון. מבחינה גיאומטרית, מדובר בזהויות הכוללות פונקציות מסוימות של זווית אחת או יותר. הם נבדלים מזהות משולש, שהם זהויות שעלולות להיות כרוכות בזוויות, אך כוללות גם אורכי צד או אורכים אחרים של משולש.
סכום הזוויות של המשולש: במרחב אוקלידי, סכום הזוויות של המשולש שווה לזווית הישר. למשולש שלוש זוויות, אחת בכל קודקוד, תחומה בזוג צלעות סמוכות.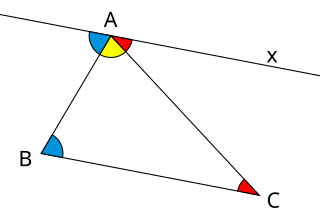
זוויות פנימיות וחיצוניות: בגיאומטריה, זווית של מצולע נוצרת על ידי שני צדדים של המצולע החולקים נקודת קצה. עבור מצולע פשוט (שאינו מצטלב עצמי), ללא קשר אם הוא קמור או לא קמור, זווית זו נקראת זווית פנימית אם נקודה בתוך הזווית נמצאת בפנים המצולע. למצולע יש בדיוק זווית פנימית אחת לקודקוד.
זוויות פנימיות וחיצוניות: בגיאומטריה, זווית של מצולע נוצרת על ידי שני צדדים של המצולע החולקים נקודת קצה. עבור מצולע פשוט (שאינו מצטלב עצמי), ללא קשר אם הוא קמור או לא קמור, זווית זו נקראת זווית פנימית אם נקודה בתוך הזווית נמצאת בפנים המצולע. למצולע יש בדיוק זווית פנימית אחת לקודקוד.
רשימת זהויות טריגונומטריות: במתמטיקה, זהויות טריגונומטריות הן שוויוניות הכוללות פונקציות טריגונומטריות ונכונות לכל ערך של המשתנים המתרחשים עבורם מוגדרים שני הצדדים של השוויון. מבחינה גיאומטרית, מדובר בזהויות הכוללות פונקציות מסוימות של זווית אחת או יותר. הם נבדלים מזהות משולש, שהם זהויות שעלולות להיות כרוכות בזוויות, אך כוללות גם אורכי צד או אורכים אחרים של משולש.
רשימת זהויות טריגונומטריות: במתמטיקה, זהויות טריגונומטריות הן שוויוניות הכוללות פונקציות טריגונומטריות ונכונות לכל ערך של המשתנים המתרחשים עבורם מוגדרים שני הצדדים של השוויון. מבחינה גיאומטרית, מדובר בזהויות הכוללות פונקציות מסוימות של זווית אחת או יותר. הם נבדלים מזהות משולש, שהם זהויות שעלולות להיות כרוכות בזוויות, אך כוללות גם אורכי צד או אורכים אחרים של משולש.
סכום הזוויות של המשולש: במרחב אוקלידי, סכום הזוויות של המשולש שווה לזווית הישר. למשולש שלוש זוויות, אחת בכל קודקוד, תחומה בזוג צלעות סמוכות.
רשימת זהויות טריגונומטריות: במתמטיקה, זהויות טריגונומטריות הן שוויוניות הכוללות פונקציות טריגונומטריות ונכונות לכל ערך של המשתנים המתרחשים עבורם מוגדרים שני הצדדים של השוויון. מבחינה גיאומטרית, מדובר בזהויות הכוללות פונקציות מסוימות של זווית אחת או יותר. הם נבדלים מזהות משולש, שהם זהויות שעלולות להיות כרוכות בזוויות, אך כוללות גם אורכי צד או אורכים אחרים של משולש.
זווית טארן (Langstrath): Angle Tarn הוא זפת מצפון לבופל ברובע האגמים האנגלי. זה מתנקז לנגסטראת 'בק.
זוויות: הזוויות היו אחד העמים הגרמניים העיקריים שהתיישבו בבריטניה בתקופה שלאחר הרומית. הם ייסדו כמה ממלכות ההפטרכיה באנגליה-סכסון, ושמם הוא שורש השם אנגליה . על פי טקיטוס, כתיבה לפני המעבר לבריטניה, זוויות התגוררו לצד לאנגוברדים וסמונות באזורים היסטוריים שלזוויג והולשטיין, שהם כיום חלק מדרום דנמרק וצפון גרמניה (שלזוויג-הולשטיין).
חיתוך זווית: חיתוך זווית הוא בעיה קלאסית של מבני מצפן וישר של המתמטיקה היוונית העתיקה. זה נוגע לבניית זווית השווה לשליש מזווית שרירותית נתונה, תוך שימוש בשני כלים בלבד: יישור לא מסומן ומצפן.
חיתוך זווית: חיתוך זווית הוא בעיה קלאסית של מבני מצפן וישר של המתמטיקה היוונית העתיקה. זה נוגע לבניית זווית השווה לשליש מזווית שרירותית נתונה, תוך שימוש בשני כלים בלבד: יישור לא מסומן ומצפן.
Chloropteryx tepperaria: Chloropteryx tepperaria , עש הברקת הזוויתית , הוא עש ממשפחת הגיאומטרידות. המין תואר לראשונה על ידי ג'ורג 'דוריה הולסט בשנת 1886 והוא נמצא בדרום-מזרח ארצות הברית.
Chloropteryx tepperaria: Chloropteryx tepperaria , עש הברקת הזוויתית , הוא עש ממשפחת הגיאומטרידות. המין תואר לראשונה על ידי ג'ורג 'דוריה הולסט בשנת 1886 והוא נמצא בדרום-מזרח ארצות הברית.
Chloropteryx tepperaria: Chloropteryx tepperaria , עש הברקת הזוויתית , הוא עש ממשפחת הגיאומטרידות. המין תואר לראשונה על ידי ג'ורג 'דוריה הולסט בשנת 1886 והוא נמצא בדרום-מזרח ארצות הברית.
Chloropteryx tepperaria: Chloropteryx tepperaria , עש הברקת הזוויתית , הוא עש ממשפחת הגיאומטרידות. המין תואר לראשונה על ידי ג'ורג 'דוריה הולסט בשנת 1886 והוא נמצא בדרום-מזרח ארצות הברית.
כדור זווית: אנגלבול הוא ארגון כושר ספורט רשום ויצרן פטנטים של ענף הספורט הוותיק ביותר בצפון אמריקה, אנאג'ודי. כללי האנג'ודי של אנגלבול הוקמו מחדש כמסורת אמריקאית במהלך מלחמת העולם השנייה באוניברסיטת בראון על ידי מאמן הכדורגל של מכללת הכדורגל ומאמן הכדורסל צ'רלס " ריפ" אנגל בכדי לשמור על כשירות אנשי מלחמת העולם השנייה האמריקאית לפני הכניסה. ציוד אנגלבול מנוהל כיום על ידי 1,000,000+ אנשים בארצות הברית ובעולם ולהתניה ב- NFL ועל ידי הספורטאים האולימפיים של קבוצת ארה"ב. מאז 2014, Angleball היוותה השראה לסוג משחק חוזר בסדרת משחקי הווידאו הנמכרת ביותר בעולם, Call of Duty, הנקראת Uplink. ל- Angleball הבינלאומי 13 מדינות חברות כיום. ארגון Angleball מכבד את מורשתו העתיקה על ידי עידוד קבוצות לייצר ציוד אנאג'ודי משלהם למדידות הפטנט של Angleball, תוך שימוש בחומרים זמינים או טבעיים, כל עוד הציוד אינו נמכר. אנגלבול הוא סימן מסחרי רשום ונמכר אך ורק על ידי חברת אנגלבול.
ז'אן הנרי ד'אנגלברט: ז'אן הנרי ד'אנגלברט היה מלחין, צ'מבלו ואורגניסט צרפתי. הוא היה אחד המלחינים המובילים בקלידים בימיו.
אנגלקוט: אנגלקוט , הידוע גם בשם בית מגורים פוטר , הוא בית מגורים היסטורי בשכונת צ'סטנאט היל בפילדלפיה, פנסילבניה, ארצות הברית. הוא תוכנן על ידי אדריכל פילדלפיה הנודע ווילסון אייר עבור צ'ארלס אדמס פוטר (1860-1925), יצרן לינוליאום.
אריאדנה אריאדנה: אריאדנה אריאדנה , הגלגל הזוויתי , הוא זן של פרפר נימפלידי שנמצא באסיה.
Allotinus fabius: Allotinus fabius , החושך הזוויתי , הוא פרפר קטן שנמצא בהודו, מיאנמר ודרום מזרח אסיה השייך למשפחת הלייקינים או הכחולים.
אנומיס סבוליפרה: אנומיס סבוליפרה (Anomis sabulifera) , הפנינה הזוויתית או חצי הלופר היוטה , היא עש ממשפחת ערבידיאה. המין תואר לראשונה על ידי אכיל גווין בשנת 1852. יש לו תפוצה פליאוטרופית והוא נע בין אפריקה מזרחה להודו, סרי לנקה ואוסטרליה. תקליט יחיד נמצא מבריטניה.
Ancylolomia chrysographellus: Ancylolomia chrysographellus , עש העשב הזוויתי , הוא זן עש במשפחת Crambidae. הוא נמצא בקפריסין ובקניה, אוגנדה, תימן, הודו, פקיסטן, סרי לנקה, מיאנמר, סין, קוריאה, יפן, טייוואן, הפיליפינים ואינדונזיה.
Eurema desjardinsii: Eurema desjardinsii , העשב הזוויתי הצהוב , הוא פרפר של המשפחה Pieridae, שנמצא באפריקה.
לופה אקוטנגולה: Luffa acutangula גדל מסחרי בזכות פירותיו הבשלים כירק. פירות בוגרים משמשים כספוגי ניקוי טבעיים. פריו דומה מעט למלפפון או קישואים עם רכסים. זה נע בין מרכז ומזרח אסיה לדרום מזרח אסיה. הוא גדל גם כצמח בית במקומות עם אקלים קר יותר. שמות נפוצים אנגלית כוללים luffa זוויתי, במיה סינית, דלעת סְמַרטוּט, דלעת חרוש, דלעת ספוג, דלעת ירקות, גפן מסננת, מצולע ליפה, דלעת כמשי, דלעת חרוש, דלעת משי, ו sinkwa towelsponge.
קלטה קלטה: Caleta caleta , הפיירוט הזוויתי , הוא זן של פרפר כחול שנמצא בסולאווסי.
ליתרום אלטום: שָׁנִית alatum, הידוע בכינויו לוססטרייף מכונף, שָׁנִית מכונף או סגול-לוססטרייף זווית, הוא מין של צמח פורח ממשפחת כופריים. הוא אנדמי באזורי ביצות במרכז ומזרח ארצות הברית ובאונטריו.
Anteos maerula: Anteos maerula , הגופרית הזוויתית או הגופרית הזוויתית הצהובה , הוא פרפר של המשפחה Pieridae. הוא נמצא מפרו למקסיקו. לעיתים נדירות ניתן למצוא מהגרים עד מזרח נברסקה, דרום מזרח אריזונה, דרום מערב ניו מקסיקו, דרום טקסס, מיסיסיפי ופלורידה.
קורטיס אקוטה: Curetis acuta , קרן השמש הזוויתית , הוא זן של פרפר השייך למשפחת הלייקנידים. הוא נמצא בתחום האינדומלאיה. Curetis acuta הוא דימורפי מבחינה מינית בשל צבע הגב השונה של הכנפיים בין המינים, אולם כנפי הגחון שלהן דומות וצבע כסף המשקף את אור השמש. השתקפות האור בכנפי הגחון הכסופים ממלאת תפקיד של איתות בזמן מעוף, הסוואה בזמן מנוחה או במצב תרדמה, והורדת טמפרטורות הגוף על ידי השתקפות אור השמש.
נמר זוויתי: הנמר הזוויתי הוא זן של פרפר נימפלידי בתת-המשפחה Danainae. הוא נמצא בפפואה גינאה החדשה ובאיי שלמה.
מִבצָר: מעוז או חומת מגן הוא מבנה הקרין החוצה מקיר הווילון של ביצור, רוב הזוויתי כלל בכושר וממוקם בפינות המבצרות. המעוז המפותח לחלוטין מורכב משני פנים ושני אגפים, כאשר האש מהאגפים יכולה להגן על קיר הווילון ועל המעוזים הסמוכים. בהשוואה לביצורים מימי הביניים שהחליפו, ביצורי המעוז הציעו מידה רבה יותר של התנגדות פסיבית ויותר מקום להגנה מטווחים בעידן הארטילריה של שריפה. כארכיטקטורה צבאית, המעוז הוא מרכיב אחד בסגנון הביצור השולט מאמצע המאה ה -16 עד אמצע המאה ה -19.
מִבצָר: מעוז או חומת מגן הוא מבנה הקרין החוצה מקיר הווילון של ביצור, רוב הזוויתי כלל בכושר וממוקם בפינות המבצרות. המעוז המפותח לחלוטין מורכב משני פנים ושני אגפים, כאשר האש מהאגפים יכולה להגן על קיר הווילון ועל המעוזים הסמוכים. בהשוואה לביצורים מימי הביניים שהחליפו, ביצורי המעוז הציעו מידה רבה יותר של התנגדות פסיבית ויותר מקום להגנה מטווחים בעידן הארטילריה של שריפה. כארכיטקטורה צבאית, המעוז הוא מרכיב אחד בסגנון הביצור השולט מאמצע המאה ה -16 עד אמצע המאה ה -19.
סוֹגֵר: סוגר הוא של שני סימני פיסוק גבוהים קדמיים או אחוריים המשמשים בדרך כלל לבידוד קטע טקסט או נתונים מסביבתו. בדרך כלל פרוס בזוגות סימטריים, סוגר בודד יכול להיות מזוהה כסוגר שמאלי או ימין או, לחלופין, סוגר זוגי פותח או סוגר זוגי סוגר , בהתאמה, בהתאם לכיווני ההקשר.
אריאדנה אריאדנה: אריאדנה אריאדנה , הגלגל הזוויתי , הוא זן של פרפר נימפלידי שנמצא באסיה.
Allotinus fabius: Allotinus fabius , החושך הזוויתי , הוא פרפר קטן שנמצא בהודו, מיאנמר ודרום מזרח אסיה השייך למשפחת הלייקינים או הכחולים.
סיפון טיסה: סיפון הטיסה של נושאת מטוסים הוא המשטח ממנו ממריאים מטוסיו ונוחתים, למעשה שדה תעופה מיניאטורי בים. בספינות ימיות קטנות יותר שאין להן תעופה כמשימה ראשונית, אזור הנחיתה למסוקים וכלי טיס מסוג VTOL אחרים מכונה גם סיפון הטיסה. המונח הרשמי של חיל הים האמריקני לספינות אלה הוא "ספינות בעלות יכולת אוויר".
אוסטה אנגולאטה: Usta angulata , הקיסר הזוויתי , הוא זן עש במשפחת Saturniidae. הוא נמצא בקניה, טנזניה, סומליה ובוצואנה.
סיפון טיסה: סיפון הטיסה של נושאת מטוסים הוא המשטח ממנו ממריאים מטוסיו ונוחתים, למעשה שדה תעופה מיניאטורי בים. בספינות ימיות קטנות יותר שאין להן תעופה כמשימה ראשונית, אזור הנחיתה למסוקים וכלי טיס מסוג VTOL אחרים מכונה גם סיפון הטיסה. המונח הרשמי של חיל הים האמריקני לספינות אלה הוא "ספינות בעלות יכולת אוויר".
אחיזה אנכית קדימה: אחיזה קדמית אנכית או אחיזה קדמית היא אחיזת אקדח אנכית המותקנת בקצה הקדמי של כלי נשק ארוך-חבית, המיועד לאחיזה ביד התמיכה הקדמית.
Cyrtodactylus angularis: Cyrtodactylus angularis , הידוע גם בכינויו שממית זוויתית קשתית או שממית יער זוויתית , הוא זן לטאה במשפחת Gekkonidae. המין אנדמי בתאילנד.
אנומיס סבוליפרה: אנומיס סבוליפרה (Anomis sabulifera) , הפנינה הזוויתית או חצי הלופר היוטה , היא עש ממשפחת ערבידיאה. המין תואר לראשונה על ידי אכיל גווין בשנת 1852. יש לו תפוצה פליאוטרופית והוא נע בין אפריקה מזרחה להודו, סרי לנקה ואוסטרליה. תקליט יחיד נמצא מבריטניה.
Ancylolomia chrysographellus: Ancylolomia chrysographellus , עש העשב הזוויתי , הוא זן עש במשפחת Crambidae. הוא נמצא בקפריסין ובקניה, אוגנדה, תימן, הודו, פקיסטן, סרי לנקה, מיאנמר, סין, קוריאה, יפן, טייוואן, הפיליפינים ואינדונזיה.
Eurema desjardinsii: Eurema desjardinsii , העשב הזוויתי הצהוב , הוא פרפר של המשפחה Pieridae, שנמצא באפריקה.
Lobelia anceps: Lobelia anceps , הידוע בכינויו לובליה זוויתית , הוא צמח עשבוני קטן ממשפחת Campanulaceae יליד מערב אוסטרליה, ניו זילנד, דרום אמריקה ודרום אפריקה.
לופה אקוטנגולה: Luffa acutangula גדל מסחרי בזכות פירותיו הבשלים כירק. פירות בוגרים משמשים כספוגי ניקוי טבעיים. פריו דומה מעט למלפפון או קישואים עם רכסים. זה נע בין מרכז ומזרח אסיה לדרום מזרח אסיה. הוא גדל גם כצמח בית במקומות עם אקלים קר יותר. שמות נפוצים אנגלית כוללים luffa זוויתי, במיה סינית, דלעת סְמַרטוּט, דלעת חרוש, דלעת ספוג, דלעת ירקות, גפן מסננת, מצולע ליפה, דלעת כמשי, דלעת חרוש, דלעת משי, ו sinkwa towelsponge.
Metarranthis angularia: מטראנטיס אנגולריה , עש המטראנטיס הזוויתי , הוא זן עש במשפחה הגיאומטרידים. הוא תואר לראשונה על ידי ויליאם בארנס וג'יימס הולידיי מקדאנוג בשנת 1917 והוא נמצא בצפון אמריקה.
פלודלה סקוורוסה: Paludella squarrosa הוא זן טחב השייך למשפחת Meesiaceae.
Lathyrus angulatus: Lathyrus angulatus הוא זן של אפונת בר הידועה בשם הנפוץ אפונה זוויתית .
נפטיס חמישון: Neptis quintilla , השייט הזעיר הזוויתי , הוא פרפר במשפחת הנימפליות. הוא נמצא בגינאה ביסאו, גינאה, סיירה לאונה, חוף השנהב, גאנה, ניגריה, קמרון, אנגולה, הרפובליקה הדמוקרטית של קונגו, אוגנדה ומערב קניה. בית הגידול מורכב משטחים פתוחים ביערות רטובים עם כיסוי חופה.
קלטה קלטה: Caleta caleta , הפיירוט הזוויתי , הוא זן של פרפר כחול שנמצא בסולאווסי.
ליתרום אלטום: שָׁנִית alatum, הידוע בכינויו לוססטרייף מכונף, שָׁנִית מכונף או סגול-לוססטרייף זווית, הוא מין של צמח פורח ממשפחת כופריים. הוא אנדמי באזורי ביצות במרכז ומזרח ארצות הברית ובאונטריו.
Epioblasma biemarginata: Epioblasma biemarginata , קליפת הרובה הזוויתית , היה זן מולים של מים מתוקים, רכיכת דו-צדדית מימית במשפחת יוניונידה, מולים הנהר. עכשיו הוא נכחד.
הטיה צירית: באסטרונומיה, הטיה צירית , המכונה גם אלכסון , היא הזווית שבין ציר הסיבוב של האובייקט לבין ציר מסלולו, או, באופן שווה, הזווית שבין מישור קו המשווה שלו למישור מסלוליו. זה שונה מנטיית מסלול.
רודודון: רודודון , המכונה מנטה חול, הוא סוג של צמח פורח במשפחת Lamiaceae, שתואר לראשונה כסוג בשנת 1939. הוא מכיל רק זן אחד ידוע, Rhododon ciliatus , מנטה החול של טקסס אנדמי למדינת טקסס בארצות הברית.
Anteos maerula: Anteos maerula , הגופרית הזוויתית או הגופרית הזוויתית הצהובה , הוא פרפר של המשפחה Pieridae. הוא נמצא מפרו למקסיקו. לעיתים נדירות ניתן למצוא מהגרים עד מזרח נברסקה, דרום מזרח אריזונה, דרום מערב ניו מקסיקו, דרום טקסס, מיסיסיפי ופלורידה.
קורטיס אקוטה: Curetis acuta , קרן השמש הזוויתית , הוא זן של פרפר השייך למשפחת הלייקנידים. הוא נמצא בתחום האינדומלאיה. Curetis acuta הוא דימורפי מבחינה מינית בשל צבע הגב השונה של הכנפיים בין המינים, אולם כנפי הגחון שלהן דומות וצבע כסף המשקף את אור השמש. השתקפות האור בכנפי הגחון הכסופים ממלאת תפקיד של איתות בזמן מעוף, הסוואה בזמן מנוחה או במצב תרדמה, והורדת טמפרטורות הגוף על ידי השתקפות אור השמש.
נמר זוויתי: הנמר הזוויתי הוא זן של פרפר נימפלידי בתת-המשפחה Danainae. הוא נמצא בפפואה גינאה החדשה ובאיי שלמה.
Scopula ancellata: Scopula ancellata , עש הגל הזוויתי או הגל המחודד , הוא עש ממשפחת הגיאומטרידות. הוא תואר על ידי ג'ורג 'דוריה הולסט בשנת 1887. הוא נמצא בצפון אמריקה מקוויבק מערבה לשטחים הצפון מערביים ובקולומביה הבריטית ודרומה למישיגן, אינדיאנה ואריזונה. בית הגידול מורכב מעץ מעורב ויערות מחטניים.
Scopula ancellata: Scopula ancellata , עש הגל הזוויתי או הגל המחודד , הוא עש ממשפחת הגיאומטרידות. הוא תואר על ידי ג'ורג 'דוריה הולסט בשנת 1887. הוא נמצא בצפון אמריקה מקוויבק מערבה לשטחים הצפון מערביים ובקולומביה הבריטית ודרומה למישיגן, אינדיאנה ואריזונה. בית הגידול מורכב מעץ מעורב ויערות מחטניים.
תלינה גיימרדי: טלינה גיימרדי , קליפת הטריז הזוויתית , היא רכיכה דו-כיוונית של המשפחה טלינידיות.
לטאת תולעת זוויתית: לטאת התולעת הזוויתית היא זן של זוחלים במשפחה Trogonophidae. הוא נמצא בסומליה בקרן אפריקה.
אנגלדול: אנגלדול הוא יישוב במערב ניו סאות 'ויילס המערבית העליונה, סמוך לגבול הדרומי של קווינסלנד, קילומטר אחד מזרחית לכביש המהיר קסטלריאג וכ 45 ק"מ צפונית לרכס ברק. במפקד האוכלוסין בשנת 2016 מנתה אנגלדול 58 אנשים.
אנגלדול: אנגלדול הוא יישוב במערב ניו סאות 'ויילס המערבית העליונה, סמוך לגבול הדרומי של קווינסלנד, קילומטר אחד מזרחית לכביש המהיר קסטלריאג וכ 45 ק"מ צפונית לרכס ברק. במפקד האוכלוסין בשנת 2016 מנתה אנגלדול 58 אנשים.