List of trigonometric identities, List of trigonometric identities, List of trigonometric identities

רשימת זהויות טריגונומטריות: במתמטיקה, זהויות טריגונומטריות הן שוויוניות הכוללות פונקציות טריגונומטריות ונכונות לכל ערך של המשתנים המתרחשים עבורם מוגדרים שני הצדדים של השוויון. מבחינה גיאומטרית, מדובר בזהויות הכוללות פונקציות מסוימות של זווית אחת או יותר. הם נבדלים מזהויות משולש, שהם זהויות שעלולות להיות כרוכות בזוויות, אך כוללות גם אורכי צד או אורכים אחרים של משולש.
רשימת זהויות טריגונומטריות: במתמטיקה, זהויות טריגונומטריות הן שוויוניות הכוללות פונקציות טריגונומטריות ונכונות לכל ערך של המשתנים המתרחשים עבורם מוגדרים שני הצדדים של השוויון. מבחינה גיאומטרית, מדובר בזהויות הכוללות פונקציות מסוימות של זווית אחת או יותר. הם נבדלים מזהויות משולש, שהם זהויות שעלולות להיות כרוכות בזוויות, אך כוללות גם אורכי צד או אורכים אחרים של משולש.
רשימת זהויות טריגונומטריות: במתמטיקה, זהויות טריגונומטריות הן שוויוניות הכוללות פונקציות טריגונומטריות ונכונות לכל ערך של המשתנים המתרחשים עבורם מוגדרים שני הצדדים של השוויון. מבחינה גיאומטרית, מדובר בזהויות הכוללות פונקציות מסוימות של זווית אחת או יותר. הם נבדלים מזהויות משולש, שהם זהויות שעלולות להיות כרוכות בזוויות, אך כוללות גם אורכי צד או אורכים אחרים של משולש.
רשימת זהויות טריגונומטריות: במתמטיקה, זהויות טריגונומטריות הן שוויוניות הכוללות פונקציות טריגונומטריות ונכונות לכל ערך של המשתנים המתרחשים עבורם מוגדרים שני הצדדים של השוויון. מבחינה גיאומטרית, מדובר בזהויות הכוללות פונקציות מסוימות של זווית אחת או יותר. הם נבדלים מזהויות משולש, שהם זהויות שעלולות להיות כרוכות בזוויות, אך כוללות גם אורכי צד או אורכים אחרים של משולש.
רשימת זהויות טריגונומטריות: במתמטיקה, זהויות טריגונומטריות הן שוויוניות הכוללות פונקציות טריגונומטריות ונכונות לכל ערך של המשתנים המתרחשים עבורם מוגדרים שני הצדדים של השוויון. מבחינה גיאומטרית, מדובר בזהויות הכוללות פונקציות מסוימות של זווית אחת או יותר. הם נבדלים מזהויות משולש, שהם זהויות שעלולות להיות כרוכות בזוויות, אך כוללות גם אורכי צד או אורכים אחרים של משולש.
רשימת זהויות טריגונומטריות: במתמטיקה, זהויות טריגונומטריות הן שוויוניות הכוללות פונקציות טריגונומטריות ונכונות לכל ערך של המשתנים המתרחשים עבורם מוגדרים שני הצדדים של השוויון. מבחינה גיאומטרית, מדובר בזהויות הכוללות פונקציות מסוימות של זווית אחת או יותר. הם נבדלים מזהויות משולש, שהם זהויות שעלולות להיות כרוכות בזוויות, אך כוללות גם אורכי צד או אורכים אחרים של משולש.
רשימת זהויות טריגונומטריות: במתמטיקה, זהויות טריגונומטריות הן שוויוניות הכוללות פונקציות טריגונומטריות ונכונות לכל ערך של המשתנים המתרחשים עבורם מוגדרים שני הצדדים של השוויון. מבחינה גיאומטרית, מדובר בזהויות הכוללות פונקציות מסוימות של זווית אחת או יותר. הם נבדלים מזהויות משולש, שהם זהויות שעלולות להיות כרוכות בזוויות, אך כוללות גם אורכי צד או אורכים אחרים של משולש.
רשימת זהויות טריגונומטריות: במתמטיקה, זהויות טריגונומטריות הן שוויוניות הכוללות פונקציות טריגונומטריות ונכונות לכל ערך של המשתנים המתרחשים עבורם מוגדרים שני הצדדים של השוויון. מבחינה גיאומטרית, מדובר בזהויות הכוללות פונקציות מסוימות של זווית אחת או יותר. הם נבדלים מזהויות משולש, שהם זהויות שעלולות להיות כרוכות בזוויות, אך כוללות גם אורכי צד או אורכים אחרים של משולש.
רשימת זהויות טריגונומטריות: במתמטיקה, זהויות טריגונומטריות הן שוויוניות הכוללות פונקציות טריגונומטריות ונכונות לכל ערך של המשתנים המתרחשים עבורם מוגדרים שני הצדדים של השוויון. מבחינה גיאומטרית, מדובר בזהויות הכוללות פונקציות מסוימות של זווית אחת או יותר. הם נבדלים מזהויות משולש, שהם זהויות שעלולות להיות כרוכות בזוויות, אך כוללות גם אורכי צד או אורכים אחרים של משולש.
רשימת זהויות טריגונומטריות: במתמטיקה, זהויות טריגונומטריות הן שוויוניות הכוללות פונקציות טריגונומטריות ונכונות לכל ערך של המשתנים המתרחשים עבורם מוגדרים שני הצדדים של השוויון. מבחינה גיאומטרית, מדובר בזהויות הכוללות פונקציות מסוימות של זווית אחת או יותר. הם נבדלים מזהויות משולש, שהם זהויות שעלולות להיות כרוכות בזוויות, אך כוללות גם אורכי צד או אורכים אחרים של משולש.
רשימת זהויות טריגונומטריות: במתמטיקה, זהויות טריגונומטריות הן שוויוניות הכוללות פונקציות טריגונומטריות ונכונות לכל ערך של המשתנים המתרחשים עבורם מוגדרים שני הצדדים של השוויון. מבחינה גיאומטרית, מדובר בזהויות הכוללות פונקציות מסוימות של זווית אחת או יותר. הם נבדלים מזהויות משולש, שהם זהויות שעלולות להיות כרוכות בזוויות, אך כוללות גם אורכי צד או אורכים אחרים של משולש.
רשימת זהויות טריגונומטריות: במתמטיקה, זהויות טריגונומטריות הן שוויוניות הכוללות פונקציות טריגונומטריות ונכונות לכל ערך של המשתנים המתרחשים עבורם מוגדרים שני הצדדים של השוויון. מבחינה גיאומטרית, מדובר בזהויות הכוללות פונקציות מסוימות של זווית אחת או יותר. הם נבדלים מזהויות משולש, שהם זהויות שעלולות להיות כרוכות בזוויות, אך כוללות גם אורכי צד או אורכים אחרים של משולש.
רשימת זהויות טריגונומטריות: במתמטיקה, זהויות טריגונומטריות הן שוויוניות הכוללות פונקציות טריגונומטריות ונכונות לכל ערך של המשתנים המתרחשים עבורם מוגדרים שני הצדדים של השוויון. מבחינה גיאומטרית, מדובר בזהויות הכוללות פונקציות מסוימות של זווית אחת או יותר. הם נבדלים מזהויות משולש, שהם זהויות שעלולות להיות כרוכות בזוויות, אך כוללות גם אורכי צד או אורכים אחרים של משולש.
רשימת זהויות טריגונומטריות: במתמטיקה, זהויות טריגונומטריות הן שוויוניות הכוללות פונקציות טריגונומטריות ונכונות לכל ערך של המשתנים המתרחשים עבורם מוגדרים שני הצדדים של השוויון. מבחינה גיאומטרית, מדובר בזהויות הכוללות פונקציות מסוימות של זווית אחת או יותר. הם נבדלים מזהויות משולש, שהם זהויות שעלולות להיות כרוכות בזוויות, אך כוללות גם אורכי צד או אורכים אחרים של משולש.
רשימת זהויות טריגונומטריות: במתמטיקה, זהויות טריגונומטריות הן שוויוניות הכוללות פונקציות טריגונומטריות ונכונות לכל ערך של המשתנים המתרחשים עבורם מוגדרים שני הצדדים של השוויון. מבחינה גיאומטרית, מדובר בזהויות הכוללות פונקציות מסוימות של זווית אחת או יותר. הם נבדלים מזהויות משולש, שהם זהויות שעלולות להיות כרוכות בזוויות, אך כוללות גם אורכי צד או אורכים אחרים של משולש.
רשימת זהויות טריגונומטריות: במתמטיקה, זהויות טריגונומטריות הן שוויוניות הכוללות פונקציות טריגונומטריות ונכונות לכל ערך של המשתנים המתרחשים עבורם מוגדרים שני הצדדים של השוויון. מבחינה גיאומטרית, מדובר בזהויות הכוללות פונקציות מסוימות של זווית אחת או יותר. הם נבדלים מזהויות משולש, שהם זהויות שעלולות להיות כרוכות בזוויות, אך כוללות גם אורכי צד או אורכים אחרים של משולש.
רשימת זהויות טריגונומטריות: במתמטיקה, זהויות טריגונומטריות הן שוויוניות הכוללות פונקציות טריגונומטריות ונכונות לכל ערך של המשתנים המתרחשים עבורם מוגדרים שני הצדדים של השוויון. מבחינה גיאומטרית, מדובר בזהויות הכוללות פונקציות מסוימות של זווית אחת או יותר. הם נבדלים מזהויות משולש, שהם זהויות שעלולות להיות כרוכות בזוויות, אך כוללות גם אורכי צד או אורכים אחרים של משולש.
רשימת זהויות טריגונומטריות: במתמטיקה, זהויות טריגונומטריות הן שוויוניות הכוללות פונקציות טריגונומטריות ונכונות לכל ערך של המשתנים המתרחשים עבורם מוגדרים שני הצדדים של השוויון. מבחינה גיאומטרית, מדובר בזהויות הכוללות פונקציות מסוימות של זווית אחת או יותר. הם נבדלים מזהויות משולש, שהם זהויות שעלולות להיות כרוכות בזוויות, אך כוללות גם אורכי צד או אורכים אחרים של משולש.
זָוִית: בגיאומטריה האוקלידית, זווית היא הדמות שנוצרת על ידי שתי קרניים, הנקראות צדי הזווית, חולקת נקודת קצה משותפת, הנקראת קודקוד הזווית. זוויות שנוצרו על ידי שתי קרניים מונחות במישור המכיל את הקרניים. זוויות נוצרות גם על ידי צומת שני מישורים. אלה נקראים זוויות דו-כיווניות. שתי עקומות מצטלבות מגדירות גם זווית, שהיא זווית המשיקים בנקודת החיתוך. לדוגמא, הזווית הכדורית הנוצרת על ידי שני עיגולים גדולים בכדור שווה לזווית הדיהדרלית בין המישורים המכילים את העיגולים הגדולים.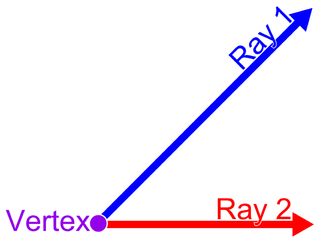
רשימת זהויות טריגונומטריות: במתמטיקה, זהויות טריגונומטריות הן שוויוניות הכוללות פונקציות טריגונומטריות ונכונות לכל ערך של המשתנים המתרחשים עבורם מוגדרים שני הצדדים של השוויון. מבחינה גיאומטרית, מדובר בזהויות הכוללות פונקציות מסוימות של זווית אחת או יותר. הם נבדלים מזהויות משולש, שהם זהויות שעלולות להיות כרוכות בזוויות, אך כוללות גם אורכי צד או אורכים אחרים של משולש.
רשימת זהויות טריגונומטריות: במתמטיקה, זהויות טריגונומטריות הן שוויוניות הכוללות פונקציות טריגונומטריות ונכונות לכל ערך של המשתנים המתרחשים עבורם מוגדרים שני הצדדים של השוויון. מבחינה גיאומטרית, מדובר בזהויות הכוללות פונקציות מסוימות של זווית אחת או יותר. הם נבדלים מזהויות משולש, שהם זהויות שעלולות להיות כרוכות בזוויות, אך כוללות גם אורכי צד או אורכים אחרים של משולש.
רשימת זהויות טריגונומטריות: במתמטיקה, זהויות טריגונומטריות הן שוויוניות הכוללות פונקציות טריגונומטריות ונכונות לכל ערך של המשתנים המתרחשים עבורם מוגדרים שני הצדדים של השוויון. מבחינה גיאומטרית, מדובר בזהויות הכוללות פונקציות מסוימות של זווית אחת או יותר. הם נבדלים מזהויות משולש, שהם זהויות שעלולות להיות כרוכות בזוויות, אך כוללות גם אורכי צד או אורכים אחרים של משולש.
רשימת זהויות טריגונומטריות: במתמטיקה, זהויות טריגונומטריות הן שוויוניות הכוללות פונקציות טריגונומטריות ונכונות לכל ערך של המשתנים המתרחשים עבורם מוגדרים שני הצדדים של השוויון. מבחינה גיאומטרית, מדובר בזהויות הכוללות פונקציות מסוימות של זווית אחת או יותר. הם נבדלים מזהויות משולש, שהם זהויות שעלולות להיות כרוכות בזוויות, אך כוללות גם אורכי צד או אורכים אחרים של משולש.
כדור זווית: אנג'לבול הוא ארגון כושר ספורט רשום ויצרן פטנטים של ענף הספורט הוותיק ביותר בצפון אמריקה, אנאג'ודי. כללי האנג'ודי של אנג'לבול הוקמו מחדש כמסורת אמריקאית במהלך מלחמת העולם השנייה באוניברסיטת בראון על ידי מאמן הכדורגל והכדורסל של מכללת היכל התהילה צ'רלס " ריפ" אנגל כדי לשמור על כשירות אנשי מלחמת העולם השנייה האמריקאית כשירות לפני ההפעלה. ציוד אנגלבול מנוהל כיום על ידי 1,000,000+ אנשים בארצות הברית ובעולם ולמיזוג ב- NFL ועל ידי ספורטאים אולימפיים של Team USA. מאז 2014, Angleball היווה השראה לסוג משחק חוזר בסדרת משחקי הווידאו הנמכרת ביותר בעולם, Call of Duty, הנקראת Uplink. ל- Angleball הבינלאומי 13 מדינות חברות כיום. ארגון Angleball מכבד את מורשתו העתיקה בכך שהוא מעודד קבוצות לייצר ציוד אנאג'ודי משלהם למדידות הפטנט של Angleball, תוך שימוש בחומרים זמינים או טבעיים, כל עוד הציוד לא נמכר. אנגלבול הוא סימן מסחרי רשום ונמכר אך ורק על ידי חברת אנגלבול.
צלחת דג: בטרמינולוגיה של מסילה, צלחת דגים , מוט שחבור או מוט משותף הם מוט מתכת המוברג בקצות שתי מסילות כדי לחבר אותם יחד למסלול. השם נגזר מדגים , מוט עץ עם פרופיל מעוקל המשמש לחיזוק תורן הספינה. הקצוות העליונים והתחתונים מתחדדים פנימה כך שהמכשיר מתרכך בין החלק העליון והתחתון של המסילה כשהוא מוברג למקומו. בדוגמנות הובלת רכבת, צלחת דג היא לרוב פלטת כסף קטנה מנחושת או מניקל המחליקה לשתי המסילות כדי לספק את הפונקציות של שמירה על יישור והמשכיות חשמלית.
חיתוך: בגיאומטריה, חיתוך הוא החלוקה של משהו לשני חלקים שווים או חופפים, בדרך כלל על ידי קו, שנקרא אז חוצה . הסוגים הנפוצים ביותר של חציית הברגים הם חציית הקטע וחצי הזווית .
משפט חציית זווית: בגיאומטריה משפט זווית הזווית עוסק באורכים היחסיים של שני הקטעים שצד משולש מחולק אליהם בקו המחצה את הזווית ההפוכה. זה משווה את אורכם היחסי לאורכים היחסיים של שני הצדדים האחרים של המשולש.
חיתוך: בגיאומטריה, חיתוך הוא החלוקה של משהו לשני חלקים שווים או חופפים, בדרך כלל על ידי קו, שנקרא אז חוצה . הסוגים הנפוצים ביותר של חציית הברגים הם חציית הקטע וחצי הזווית .
סוֹגֵר: סוגר הוא אחד משני סימני פיסוק גבוהים לפנים או לאחור הפונים בדרך כלל לבידוד קטע טקסט או נתונים מסביבתו. בדרך כלל פרוס בזוגות סימטריים, סוגר בודד עשוי להיות מזוהה שמאל או סוגר תקין או, לחלופין, סוגרים זיווג פתיחה או סגירת זיווג סוגר, בהתאמה, בהתאם הכיווניות של ההקשר.
סוגר זווית (אטב): סוגר זווית או סוגר זווית או זווית זווית הוא אטב בצורת L המשמש לחיבור שני חלקים בדרך כלל בזווית של 90 מעלות. הוא עשוי בדרך כלל ממתכת, אך הוא יכול גם להיות עשוי עץ או פלסטיק. בסוגרי הזווית המתכתיים יש חורים בהם לברגים. השימוש האופייני בו הוא לחבר מדף עץ לקיר או לחבר שני חלקי ריהוט יחד.
סוֹגֵר: סוגר הוא אחד משני סימני פיסוק גבוהים לפנים או לאחור הפונים בדרך כלל לבידוד קטע טקסט או נתונים מסביבתו. בדרך כלל פרוס בזוגות סימטריים, סוגר בודד עשוי להיות מזוהה שמאל או סוגר תקין או, לחלופין, סוגרים זיווג פתיחה או סגירת זיווג סוגר, בהתאמה, בהתאם הכיווניות של ההקשר.
סוֹגֵר: סוגר הוא אחד משני סימני פיסוק גבוהים לפנים או לאחור הפונים בדרך כלל לבידוד קטע טקסט או נתונים מסביבתו. בדרך כלל פרוס בזוגות סימטריים, סוגר בודד עשוי להיות מזוהה שמאל או סוגר תקין או, לחלופין, סוגרים זיווג פתיחה או סגירת זיווג סוגר, בהתאמה, בהתאם הכיווניות של ההקשר.
רשימת הז'רגון המתמטי: לשפת המתמטיקה אוצר מילים עצום של מונחים מומחים וטכניים. יש לו גם כמות מסוימת של ז'רגון: ביטויים נפוצים שהם חלק מתרבות המתמטיקה, ולא מהנושא. ז'רגון מופיע לעתים קרובות בהרצאות, ולעתים בדפוס, כקצרנות בלתי פורמלית לוויכוחים קפדניים או רעיונות מדויקים. הרבה מכך הוא אנגלית נפוצה, אך עם משמעות ספציפית שאינה ברורה מאליה כאשר משתמשים בה במתמטיקה.
רשימת הז'רגון המתמטי: לשפת המתמטיקה אוצר מילים עצום של מונחים מומחים וטכניים. יש לו גם כמות מסוימת של ז'רגון: ביטויים נפוצים שהם חלק מתרבות המתמטיקה, ולא מהנושא. ז'רגון מופיע לעתים קרובות בהרצאות, ולעתים בדפוס, כקצרנות בלתי פורמלית לוויכוחים קפדניים או רעיונות מדויקים. הרבה מכך הוא אנגלית נפוצה, אך עם משמעות ספציפית שאינה ברורה מאליה כאשר משתמשים בה במתמטיקה.
בַּרקִית: גלאוקומה היא קבוצה של מחלות עיניים אשר גורמות לפגיעה בעצב הראייה וגורמות לאובדן ראייה. הסוג הנפוץ ביותר הוא גלאוקומה בזווית פתוחה , בה זווית הניקוז של נוזלים בעין נותרת פתוחה, עם סוגים פחות נפוצים כולל גלאוקומה בזווית סגורה וגלאוקומה במתח רגיל. גלאוקומה בזווית פתוחה מתפתחת באטיות לאורך זמן ואין כאב. הראייה ההיקפית עשויה להתחיל לרדת, ואחריה הראייה המרכזית, וכתוצאה מכך עיוורון אם אינו מטופל. גלאוקומה של זווית סגורה יכולה להופיע בהדרגה או בפתאומיות. המצגת הפתאומית עשויה להיות כרוכה בכאבי עיניים חזקים, טשטוש ראייה, אישון מורחב באמצע, אדמומיות בעין ובחילה. אובדן הראייה מגלאוקומה, ברגע שהוא התרחש, הוא קבוע. עיניים המושפעות מגלאוקומה מכונות גלאוקומטיות .
בַּרקִית: גלאוקומה היא קבוצה של מחלות עיניים אשר גורמות לפגיעה בעצב הראייה וגורמות לאובדן ראייה. הסוג הנפוץ ביותר הוא גלאוקומה בזווית פתוחה , בה זווית הניקוז של נוזלים בעין נותרת פתוחה, עם סוגים פחות נפוצים כולל גלאוקומה בזווית סגורה וגלאוקומה במתח רגיל. גלאוקומה בזווית פתוחה מתפתחת באטיות לאורך זמן ואין כאב. הראייה ההיקפית עשויה להתחיל לרדת, ואחריה הראייה המרכזית, וכתוצאה מכך עיוורון אם אינו מטופל. גלאוקומה של זווית סגורה יכולה להופיע בהדרגה או בפתאומיות. המצגת הפתאומית עשויה להיות כרוכה בכאבי עיניים חזקים, טשטוש ראייה, אישון מורחב באמצע, אדמומיות בעין ובחילה. אובדן הראייה מגלאוקומה, ברגע שהוא התרחש, הוא קבוע. עיניים המושפעות מגלאוקומה מכונות גלאוקומטיות .
מצב זווית: במתמטיקה, תנאי הזווית הוא אילוץ המסופק על ידי מוקד הנקודות במישור ה- s שעליו שוכנים קטבי לולאה סגורה של מערכת. בשילוב עם מצב הגודל, שני הביטויים המתמטיים הללו קובעים באופן מלא את מקום השורש.
שיבוש הונאת זווית: שיבוש הונאת זווית הוא טכניקת לוחמה אלקטרונית המשמשת כנגד מערכות מכ"ם סריקות חרוטיות. זה יוצר אות כוזב השוטה את המכ"ם להאמין שהמטרה היא לצד אחד של הראייה, וגורם לרדאר "להתרחק" מהיעד ולשבור את נעילת הרדאר שלו. זה ידוע גם בשם זווית זווית , גניבת זווית או סריקה הפוכה .
פגם זוויתי: בגיאומטריה, הפגם ( הזוויתי ) פירושו כישלון של כמה זוויות להסתכם בכמות הצפויה של 360 ° או 180 °, כאשר זוויות כאלה במישור האוקלידי היו. הרעיון ההפוך הוא העודף.
אוטוקולימולטור: אוטוקולימולטור הוא מכשיר אופטי למדידת זוויות ללא מגע. הם משמשים בדרך כלל ליישור רכיבים ומדידת סטיות במערכות אופטיות או מכניות. אוטוקולימולטור עובד על ידי הקרנת תמונה על מראה מטרה ומדידת סטיה של התמונה המוחזרת על פי קנה מידה, באופן ויזואלי או באמצעות גלאי אלקטרוני. אוטו-קולימולטור ויזואלי יכול למדוד זוויות קטנות לשנייה אחת, ואילו למוליך אוטומטי אלקטרוני יכול להיות רזולוציה גבוהה פי 100.
רשימת זהויות טריגונומטריות: במתמטיקה, זהויות טריגונומטריות הן שוויוניות הכוללות פונקציות טריגונומטריות ונכונות לכל ערך של המשתנים המתרחשים עבורם מוגדרים שני הצדדים של השוויון. מבחינה גיאומטרית, מדובר בזהויות הכוללות פונקציות מסוימות של זווית אחת או יותר. הם נבדלים מזהויות משולש, שהם זהויות שעלולות להיות כרוכות בזוויות, אך כוללות גם אורכי צד או אורכים אחרים של משולש.
רשימת זהויות טריגונומטריות: במתמטיקה, זהויות טריגונומטריות הן שוויוניות הכוללות פונקציות טריגונומטריות ונכונות לכל ערך של המשתנים המתרחשים עבורם מוגדרים שני הצדדים של השוויון. מבחינה גיאומטרית, מדובר בזהויות הכוללות פונקציות מסוימות של זווית אחת או יותר. הם נבדלים מזהויות משולש, שהם זהויות שעלולות להיות כרוכות בזוויות, אך כוללות גם אורכי צד או אורכים אחרים של משולש.
רשימת זהויות טריגונומטריות: במתמטיקה, זהויות טריגונומטריות הן שוויוניות הכוללות פונקציות טריגונומטריות ונכונות לכל ערך של המשתנים המתרחשים עבורם מוגדרים שני הצדדים של השוויון. מבחינה גיאומטרית, מדובר בזהויות הכוללות פונקציות מסוימות של זווית אחת או יותר. הם נבדלים מזהויות משולש, שהם זהויות שעלולות להיות כרוכות בזוויות, אך כוללות גם אורכי צד או אורכים אחרים של משולש.
רשימת זהויות טריגונומטריות: במתמטיקה, זהויות טריגונומטריות הן שוויוניות הכוללות פונקציות טריגונומטריות ונכונות לכל ערך של המשתנים המתרחשים עבורם מוגדרים שני הצדדים של השוויון. מבחינה גיאומטרית, מדובר בזהויות הכוללות פונקציות מסוימות של זווית אחת או יותר. הם נבדלים מזהויות משולש, שהם זהויות שעלולות להיות כרוכות בזוויות, אך כוללות גם אורכי צד או אורכים אחרים של משולש.
רשימת זהויות טריגונומטריות: במתמטיקה, זהויות טריגונומטריות הן שוויוניות הכוללות פונקציות טריגונומטריות ונכונות לכל ערך של המשתנים המתרחשים עבורם מוגדרים שני הצדדים של השוויון. מבחינה גיאומטרית, מדובר בזהויות הכוללות פונקציות מסוימות של זווית אחת או יותר. הם נבדלים מזהויות משולש, שהם זהויות שעלולות להיות כרוכות בזוויות, אך כוללות גם אורכי צד או אורכים אחרים של משולש.
רשימת זהויות טריגונומטריות: במתמטיקה, זהויות טריגונומטריות הן שוויוניות הכוללות פונקציות טריגונומטריות ונכונות לכל ערך של המשתנים המתרחשים עבורם מוגדרים שני הצדדים של השוויון. מבחינה גיאומטרית, מדובר בזהויות הכוללות פונקציות מסוימות של זווית אחת או יותר. הם נבדלים מזהויות משולש, שהם זהויות שעלולות להיות כרוכות בזוויות, אך כוללות גם אורכי צד או אורכים אחרים של משולש.
רשימת זהויות טריגונומטריות: במתמטיקה, זהויות טריגונומטריות הן שוויוניות הכוללות פונקציות טריגונומטריות ונכונות לכל ערך של המשתנים המתרחשים עבורם מוגדרים שני הצדדים של השוויון. מבחינה גיאומטרית, מדובר בזהויות הכוללות פונקציות מסוימות של זווית אחת או יותר. הם נבדלים מזהויות משולש, שהם זהויות שעלולות להיות כרוכות בזוויות, אך כוללות גם אורכי צד או אורכים אחרים של משולש.
רשימת זהויות טריגונומטריות: במתמטיקה, זהויות טריגונומטריות הן שוויוניות הכוללות פונקציות טריגונומטריות ונכונות לכל ערך של המשתנים המתרחשים עבורם מוגדרים שני הצדדים של השוויון. מבחינה גיאומטרית, מדובר בזהויות הכוללות פונקציות מסוימות של זווית אחת או יותר. הם נבדלים מזהויות משולש, שהם זהויות שעלולות להיות כרוכות בזוויות, אך כוללות גם אורכי צד או אורכים אחרים של משולש.
רשימת זהויות טריגונומטריות: במתמטיקה, זהויות טריגונומטריות הן שוויוניות הכוללות פונקציות טריגונומטריות ונכונות לכל ערך של המשתנים המתרחשים עבורם מוגדרים שני הצדדים של השוויון. מבחינה גיאומטרית, מדובר בזהויות הכוללות פונקציות מסוימות של זווית אחת או יותר. הם נבדלים מזהויות משולש, שהם זהויות שעלולות להיות כרוכות בזוויות, אך כוללות גם אורכי צד או אורכים אחרים של משולש.
רשימת זהויות טריגונומטריות: במתמטיקה, זהויות טריגונומטריות הן שוויוניות הכוללות פונקציות טריגונומטריות ונכונות לכל ערך של המשתנים המתרחשים עבורם מוגדרים שני הצדדים של השוויון. מבחינה גיאומטרית, מדובר בזהויות הכוללות פונקציות מסוימות של זווית אחת או יותר. הם נבדלים מזהויות משולש, שהם זהויות שעלולות להיות כרוכות בזוויות, אך כוללות גם אורכי צד או אורכים אחרים של משולש.
רשימת זהויות טריגונומטריות: במתמטיקה, זהויות טריגונומטריות הן שוויוניות הכוללות פונקציות טריגונומטריות ונכונות לכל ערך של המשתנים המתרחשים עבורם מוגדרים שני הצדדים של השוויון. מבחינה גיאומטרית, מדובר בזהויות הכוללות פונקציות מסוימות של זווית אחת או יותר. הם נבדלים מזהויות משולש, שהם זהויות שעלולות להיות כרוכות בזוויות, אך כוללות גם אורכי צד או אורכים אחרים של משולש.
רשימת זהויות טריגונומטריות: במתמטיקה, זהויות טריגונומטריות הן שוויוניות הכוללות פונקציות טריגונומטריות ונכונות לכל ערך של המשתנים המתרחשים עבורם מוגדרים שני הצדדים של השוויון. מבחינה גיאומטרית, מדובר בזהויות הכוללות פונקציות מסוימות של זווית אחת או יותר. הם נבדלים מזהויות משולש, שהם זהויות שעלולות להיות כרוכות בזוויות, אך כוללות גם אורכי צד או אורכים אחרים של משולש.
רשימת זהויות טריגונומטריות: במתמטיקה, זהויות טריגונומטריות הן שוויוניות הכוללות פונקציות טריגונומטריות ונכונות לכל ערך של המשתנים המתרחשים עבורם מוגדרים שני הצדדים של השוויון. מבחינה גיאומטרית, מדובר בזהויות הכוללות פונקציות מסוימות של זווית אחת או יותר. הם נבדלים מזהויות משולש, שהם זהויות שעלולות להיות כרוכות בזוויות, אך כוללות גם אורכי צד או אורכים אחרים של משולש.
טריגונומטריה כדורית: טריגונומטריה כדורית היא ענף הגיאומטריה הכדורית העוסק ביחסים בין פונקציות טריגונומטריות של הצדדים לזוויות המצולעים הכדוריים המוגדרים על ידי מספר מעגלים גדולים המצטלבים בכדור. לטריגונומטריה כדורית חשיבות רבה לחישובים באסטרונומיה, גיאודזיה וניווט.
פונקציות טריגונומטריות: במתמטיקה, הפונקציות הטריגונומטריות הן פונקציות אמיתיות המתייחסות לזווית של משולש ישר ויחסים של שני אורכי צד. הם נמצאים בשימוש נרחב בכל המדעים שקשורים לגיאומטריה, כגון ניווט, מכניקה מוצקה, מכניקה שמימית, גיאודזיה ורבים אחרים. הם נמנים עם הפונקציות התקופתיות הפשוטות ביותר, וככאלה משמשים גם באופן נרחב לחקר תופעות תקופתיות באמצעות ניתוח פורייה.
פונקציות טריגונומטריות: במתמטיקה, הפונקציות הטריגונומטריות הן פונקציות אמיתיות המתייחסות לזווית של משולש ישר ויחסים של שני אורכי צד. הם נמצאים בשימוש נרחב בכל המדעים שקשורים לגיאומטריה, כגון ניווט, מכניקה מוצקה, מכניקה שמימית, גיאודזיה ורבים אחרים. הם נמנים עם הפונקציות התקופתיות הפשוטות ביותר, וככאלה משמשים גם באופן נרחב לחקר תופעות תקופתיות באמצעות ניתוח פורייה.
ביליארד עם שלוש כריות: ביליארד בעל שלוש כריות , הנקרא גם כרום שלוש כריות , הוא צורה פופולרית של ביליארד של קרומים.
מד זווית: מד זווית הוא כלי המשמש את היערנים לקביעת אילו עצים למדוד כאשר משתמשים בעיצוב חלקות ברדיוס משתנה במלאי היער. באמצעות כלי זה יכול יער למדוד במהירות את העצים שנמצאים בתוך החלקה או מחוצה לה. מד זווית דומה למנסרת טריז אם כי יש להחזיקו מרחק קבוע מהעין כדי לעבוד כראוי. שלא כמו מנסרת הטריז, המוחזקת מעל מרכז העלילה, עין המודד נשמרת מעל מרכז העלילה כאשר משתמשים במד זווית.
דיסק חיתוך: מטחנת זווית , המכונה גם מטחנה צדדית או מטחנת דיסק , היא כלי חשמל כף יד המשמש לטחינה ולליטוש. למרות שפותח במקור ככלי לדיסקים שוחקים קשיחים, הזמינות של מקור כוח מתחלף עודדה את השימוש בהם עם מגוון רחב של חותכים ותוספים.
Acradenia euodiiformis: Acradenia euodiiformis , הידוע בכינויו לב סאטן צהוב או עץ עצם עצם , הוא מין עץ אנדמי במזרח אוסטרליה. יש בו בעיקר עלים משולשים, העלונים צרים אליפטי בצורת אורך, עם בלוטות שמן בולטות, ופנימיות של פרחים לבנים. הוא צומח ביערות הגשם ובסמוך לו.
משפט תאלס: בגיאומטריה, משפט תאלס קובע שאם A, B ו- C הן נקודות מובחנות במעגל שבו הקו AC הוא קוטר, הזווית ABC היא זווית ישרה. משפט תאלס הוא מקרה מיוחד של משפט הזווית הכתובה והוא מוזכר והוכח כחלק מההצעה ה -31 בספר השלישי של אלמנטים של אוקלידס. בדרך כלל מייחסים אותו לתאלס ממילטוס אבל לפעמים מייחסים אותו לפיתגורס.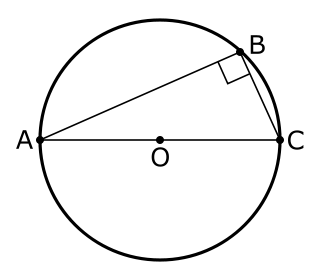
משפט תאלס: בגיאומטריה, משפט תאלס קובע שאם A, B ו- C הן נקודות מובחנות במעגל שבו הקו AC הוא קוטר, הזווית ABC היא זווית ישרה. משפט תאלס הוא מקרה מיוחד של משפט הזווית הכתובה והוא מוזכר והוכח כחלק מההצעה ה -31 בספר השלישי של אלמנטים של אוקלידס. בדרך כלל מייחסים אותו לתאלס ממילטוס אבל לפעמים מייחסים אותו לפיתגורס.
משקיע אנג'ל: משקיע אנג'ל הוא אדם המספק הון להקמת עסק, בדרך כלל תמורת חוב להמרה או הון עצמי. משקיעי אנג'ל בדרך כלל נותנים תמיכה לסטארט-אפים ברגעים הראשוניים וכשמרבית המשקיעים אינם מוכנים לגבות אותם. מספר קטן אך הולך וגדל של משקיעי אנג'ל משקיעים באופן מקוון באמצעות מימון המונים הוני או מארגנים את עצמם בקבוצות מלאכים או ברשתות אנג'לים כדי לחלוק הון השקעה, כמו גם כדי לספק ייעוץ לחברות הפורטפוליו שלהם. במהלך 50 השנים האחרונות מספר המשקיעים באנג'ל גדל מאוד.
פלדה מבנית: פלדה מבנית היא קטגוריית פלדה המשמשת לייצור חומרי בניין במגוון צורות. צורות פלדה מבניות רבות לובשות צורה של קרן מוארכת בעלת פרופיל של חתך ספציפי. צורות פלדה, גדלים, הרכב כימי, תכונות מכניות כגון חוזקות, נוהלי אחסון וכו 'מוסדרים על ידי תקנים ברוב המדינות המתועשות.
אגם זווית: Angle Lake יכול להתייחס ל: Lake Angle, אלברטה, אזור לא מאוגד בקנדה אגם זווית (אלברטה), אגם בקנדה אגם זווית בעיירת זווית, אגם מחוז וודס, מינסוטה בארצות הברית Angle Lake, וושינגטון, ב SeaTac, וושינגטון תחנת Angle Lake, תחנת מעבר ברכבת בסיטאק, וושינגטון
Acacia truncata: Acacia truncata , הידוע בכינויו זווית עלים זוויתית או וואטל החוף המערבי , הוא שיח חוף במשפחת Fabaceae, עם תפוצה מקומית לאורך החוף הדרום-מערבי של מערב אוסטרליה. דגימה של ואטל זה היה חלק מאוסף בוטני אירופי מוקדם, אולי הראשון מאוסטרליה.
Acacia truncata: Acacia truncata , הידוע בכינויו זווית עלים זוויתית או וואטל החוף המערבי , הוא שיח חוף במשפחת Fabaceae, עם תפוצה מקומית לאורך החוף הדרום-מערבי של מערב אוסטרליה. דגימה של ואטל זה היה חלק מאוסף בוטני אירופי מוקדם, אולי הראשון מאוסטרליה.
תחנת סירת הצלה זווית: תחנת Angle Lifelat , Angle, Pembrokeshire, וויילס, נפתחה לראשונה בשנת 1868 לאחר בקשת משמר החוף המקומי לפתוח תחנת סירות הצלה בתוך נתיב המים של מילפורד הייבן. במקור נקראה תחנת הצלת סירות הצלה מילפורד , בשנת 1892 השם שונה רשמית על ידי הוועדה המלכותית הלאומית להצלת סירות (RNLI).
מידת זווית:
זָוִית: בגיאומטריה האוקלידית, זווית היא הדמות שנוצרת על ידי שתי קרניים, הנקראות צדי הזווית, חולקת נקודת קצה משותפת, הנקראת קודקוד הזווית. זוויות שנוצרו על ידי שתי קרניים מונחות במישור המכיל את הקרניים. זוויות נוצרות גם על ידי צומת שני מישורים. אלה נקראים זוויות דו-כיווניות. שתי עקומות מצטלבות מגדירות גם זווית, שהיא זווית המשיקים בנקודת החיתוך. לדוגמא, הזווית הכדורית הנוצרת על ידי שני עיגולים גדולים בכדור שווה לזווית הדיהדרלית בין המישורים המכילים את העיגולים הגדולים.
כלי מדידה: מכשיר מדידה הוא מכשיר למדידת כמות פיזית. במדעי הפיסיקה, אבטחת האיכות וההנדסה, המדידה היא פעילות השגת והשוואה בין כמויות פיזיות של עצמים ואירועים בעולם האמיתי. עצמים ואירועים סטנדרטיים מבוססים משמשים כיחידות, ותהליך המדידה נותן מספר המתייחס לפריט הנחקר ויחידת המידה המפנית אליו. מכשירי מדידה ושיטות בדיקה פורמליות המגדירות את השימוש במכשיר, הם האמצעים שבהם מתקבלים יחסי מספרים אלה. כל מכשירי המדידה כפופים לדרגות שונות של שגיאות מכשירים ואי וודאות מדידה. מכשירים אלה עשויים לנוע בין עצמים פשוטים כגון סרגלים ושעוני עצירה למיקרוסקופים אלקטרוניים ומאיצי חלקיקים. מכשור וירטואלי נמצא בשימוש נרחב בפיתוח מכשירי מדידה מודרניים.
כלי מדידה: מכשיר מדידה הוא מכשיר למדידת כמות פיזית. במדעי הפיסיקה, אבטחת האיכות וההנדסה, המדידה היא פעילות השגת והשוואה בין כמויות פיזיות של עצמים ואירועים בעולם האמיתי. עצמים ואירועים סטנדרטיים מבוססים משמשים כיחידות, ותהליך המדידה נותן מספר המתייחס לפריט הנחקר ויחידת המידה המפנית אליו. מכשירי מדידה ושיטות בדיקה פורמליות המגדירות את השימוש במכשיר, הם האמצעים שבהם מתקבלים יחסי מספרים אלה. כל מכשירי המדידה כפופים לדרגות שונות של שגיאות מכשירים ואי וודאות מדידה. מכשירים אלה עשויים לנוע בין עצמים פשוטים כגון סרגלים ושעוני עצירה למיקרוסקופים אלקטרוניים ומאיצי חלקיקים. מכשור וירטואלי נמצא בשימוש נרחב בפיתוח מכשירי מדידה מודרניים.
אפנון זווית: אפנון זווית הוא סוג של אפנון מוביל המשמש במערכות שידור טלקומוניקציה. הכיתה כוללת אפנון תדרים (FM) ואפנון פאזה (PM), והיא מבוססת על שינוי התדר או השלב, בהתאמה, של אות הספק לקידוד אות ההודעה. זה מנוגד לשינוי המשרעת של המוביל, הנהוג בהעברת אפנון משרעת (AM), המוקדם מבין שיטות האפנון העיקריות ששימשו באופן נרחב בשידורי רדיו מוקדמים.
פאזור: בפיזיקה והנדסה, פאזור , הוא מספר מורכב המייצג פונקציה סינוסואידית שמשרעתה ( A ), תדירות הזווית ( ω ), והשלב הראשוני ( θ ) אינם משתנים בזמן. זה קשור למושג כללי יותר שנקרא ייצוג אנליטי, שמפרק סינוסואיד לתוצר של קבוע מורכב וגורם בהתאם לזמן ולתדירות. קבוע המורכב, אשר תלוי המשרעת והפאזה, שמכונה פאזור, או משרעת מורכבת, ועל sinor או complexor אפילו.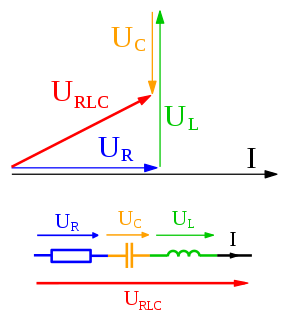
זווית ההגעה: זווית ההגעה ( AoA ) של האות היא הכיוון ממנו מתקבל האות.
זווית התקפה: בדינמיקה של נוזלים, זווית ההתקפה היא הזווית שבין קו התייחסות בגוף לבין הווקטור המייצג את התנועה היחסית בין הגוף לנוזל שדרכו הוא נע. זווית ההתקפה היא הזווית שבין קו הייחוס של הגוף לזרימה הקרובה. מאמר זה מתמקד ביישום הנפוץ ביותר, בזווית ההתקפה של כנף או נייר שנע באוויר.
זווית הטיפוס: באווירודינמיקה, שיפוע הטיפוס הוא היחס בין מרחק הנסיעה על פני הקרקע לגובה שנצבר, ומתבטא באחוזים. ניתן להגדיר את זווית הטיפוס כזווית בין מישור אופקי המייצג את פני כדור הארץ לבין נתיב הטיסה בפועל ואחריו המטוס במהלך עלייתו.
זווית הכניסה: Angle of Entry הוא אלבום אקוסטי חי בהיקף מוגבל שהוקלט על ידי ציפורני הבשר במהלך הופעתם של Envy of Angels בבריטניה בשנת 1997 ושוחרר בלייבל המנהלים שלהם. הוא נמכר בהופעות ובאינטרנט.
זווית שלו: הזווית שלו , הידועה גם בשם זווית הוושט , היא הזווית החריפה שנוצרת בין הקרדיה בכניסה לקיבה לוושט. זה עוזר במניעת ריפלוקס חומצי של חומצת קיבה לוושט. זה בדרך כלל לא מפותח אצל תינוקות, מה שהופך את הריפלוקס החומצי לשכיח יותר.
זָוִית פְּגִיעָה: זווית ההיארעות היא מדד לסטייה של משהו מ"ישר ", והיא עשויה להתייחס ל: זווית הפגיעה (אווירודינמיקה), זווית בין אקורד כנף לציר האורך, להבדיל מזווית ההתקפה, שהיא יחסית לזרימת האוויר. זווית ההיארעות (אופטיקה), המתארת ​​את התקרבות הקרן למשטח
זווית פנימית: הזווית בחזה היא המפרק הסינארטרוטי שנוצר על ידי המפרק של המנוברום וגוף עצם החזה.
זווית פנימית: הזווית בחזה היא המפרק הסינארטרוטי שנוצר על ידי המפרק של המנוברום וגוף עצם החזה.
השתקפות (פיזיקה): השתקפות היא שינוי כיוון חזית הגל בממשק בין שני מדיות שונות כך שחזית הגל חוזרת למדיום שממנו מקורו. דוגמאות נפוצות כוללות השתקפות גלי אור, קול ומים. חוק ההשתקפות אומר כי לצורך השתקפות ספקולרית הזווית בה הגל נופל על פני השטח שווה לזווית בה הוא משתקף. מראות מציגות השתקפות ספקולרית.
החוק של סנל: החוק של סנל הוא נוסחה המשמשת לתיאור הקשר בין זוויות השכיחות והשבירה, כאשר מתייחסים לאור או לגלים אחרים העוברים דרך גבול בין שני מדיות איזוטרופיות שונות, כגון מים, זכוכית או אוויר.
זווית המנוחה: זווית המנוחה הוא רומן משנת 1971 מאת וואלאס שטגנר על היסטוריון שמשתמש בכיסא גלגלים, לימן וורד, שאיבד את הקשר עם בנו ומשפחתו החיה ומחליט לכתוב על סביו מתקופת הגבול. הוא זכה בפרס פוליצר לסיפורת בשנת 1972. הרומן מבוסס ישירות על מכתביה של מרי הולוק פוט, שפורסמו מאוחר יותר כג'נטלמן ויקטוריאנית במערב הרחוק .
זווית המנוחה: זווית המנוחה הוא רומן משנת 1971 מאת וואלאס שטגנר על היסטוריון שמשתמש בכיסא גלגלים, לימן וורד, שאיבד את הקשר עם בנו ומשפחתו החיה ומחליט לכתוב על סביו מתקופת הגבול. הוא זכה בפרס פוליצר לסיפורת בשנת 1972. הרומן מבוסס ישירות על מכתביה של מרי הולוק פוט, שפורסמו מאוחר יותר כג'נטלמן ויקטוריאנית במערב הרחוק .
גבול היציבות החיובית: גבול היציבות החיובית (LPS) או זווית היציבות הנעלמת (AVS) היא הזווית מהאנכי בו סירה כבר לא תישאר זקופה אלא תתהפך, תהפוך או הפוכה.
בן לרנר: בנג'מין ס 'לרנר הוא משורר, סופר, מסאי ומבקר אמריקאי. הוא היה מלומד פולברייט, גמר בפרס פוליצר לסיפורת, גמר בפרס הספר הלאומי, גמר בפרס מעגל מבקרי הספרים הלאומי, עמית קרן הווארד, עמית גוגנהיים ועמית מקארתור, בין היתר. הצטיינות. בשנת 2011 הוא זכה ב- "Preis der Stadt Münster für internationale Poesie", האמריקאי הראשון שזכה בכבוד. לרנר מלמד בקולג 'ברוקלין, שם מונה לפרופסור מכובד לאנגלית בשנת 2016.
זוויות גישה ויציאה: זווית הגישה היא הזווית המקסימלית של רמפה עליה יכול רכב לטפס ממישור אופקי ללא הפרעה. הוא מוגדר כזווית בין הקרקע לקו הנמתח בין הצמיג הקדמי לחלק התלוי הנמוך ביותר ברכב בקיר הקדמי. זווית היציאה היא מקבילה בחלק האחורי של הרכב - זווית הרמפה המקסימלית שממנה יכולה המכונית לרדת ללא נזק. זוויות גישה וגישה נקראות גם זוויות רמפה .
זווית ההגעה: זווית ההגעה ( AoA ) של האות היא הכיוון ממנו מתקבל האות.
זווית התקפה: בדינמיקה של נוזלים, זווית ההתקפה היא הזווית שבין קו התייחסות בגוף לבין הווקטור המייצג את התנועה היחסית בין הגוף לנוזל שדרכו הוא נע. זווית ההתקפה היא הזווית שבין קו הייחוס של הגוף לזרימה הקרובה. מאמר זה מתמקד ביישום הנפוץ ביותר, בזווית ההתקפה של כנף או נייר שנע באוויר.
זווית התקפה: בדינמיקה של נוזלים, זווית ההתקפה היא הזווית שבין קו התייחסות בגוף לבין הווקטור המייצג את התנועה היחסית בין הגוף לנוזל שדרכו הוא נע. זווית ההתקפה היא הזווית שבין קו הייחוס של הגוף לזרימה הקרובה. מאמר זה מתמקד ביישום הנפוץ ביותר, בזווית ההתקפה של כנף או נייר שנע באוויר.
זווית התקפה: בדינמיקה של נוזלים, זווית ההתקפה היא הזווית שבין קו התייחסות בגוף לבין הווקטור המייצג את התנועה היחסית בין הגוף לנוזל שדרכו הוא נע. זווית ההתקפה היא הזווית שבין קו הייחוס של הגוף לזרימה הקרובה. מאמר זה מתמקד ביישום הנפוץ ביותר, בזווית ההתקפה של כנף או נייר שנע באוויר.
אַזִימוּט: אזימוט הוא מדידה זוויתית במערכת קואורדינטות כדורית. הווקטור ממתבונן (מוצא) לנקודת עניין מוקרן בניצב על מישור התייחסות; הזווית בין הווקטור המוקרן לווקטור התייחסות במישור הייחוס נקראת אזימוט.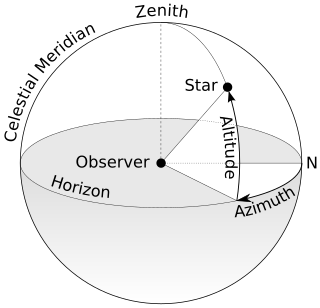
תור בנקאי: סיבוב בנקאי הוא סיבוב או שינוי כיוון בו הרכב מתנשא או נוטה, בדרך כלל לכיוון החלק הפנימי של הסיבוב. בכביש או ברכבת זה בדרך כלל נובע מכך שיש לאדמת הכביש שיפוע רוחבי כלפי פנים העקומה. זווית הבנק היא הזווית בה נוטה הרכב סביב ציר האורך שלו ביחס לאופק.
זווית הטיפוס: באווירודינמיקה, שיפוע הטיפוס הוא היחס בין מרחק הנסיעה על פני הקרקע לגובה שנצבר, ומתבטא באחוזים. ניתן להגדיר את זווית הטיפוס כזווית בין מישור אופקי המייצג את פני כדור הארץ לבין נתיב הטיסה בפועל ואחריו המטוס במהלך עלייתו.
דחייה: באסטרונומיה, נטייה היא אחת משתי הזוויות המאתרות נקודה על הכדור השמימי במערכת הקואורדינטות המשווניות, והשנייה היא זווית שעה. זווית הטיה נמדדת מצפון או מדרום לקו המשווה השמימי, לאורך מעגל השעה שעובר בנקודה הנדונה.
זוויות גישה ויציאה: זווית הגישה היא הזווית המקסימלית של רמפה עליה יכול רכב לטפס ממישור אופקי ללא הפרעה. הוא מוגדר כזווית בין הקרקע לקו הנמתח בין הצמיג הקדמי לחלק התלוי הנמוך ביותר ברכב בקיר הקדמי. זווית היציאה היא מקבילה בחלק האחורי של הרכב - זווית הרמפה המקסימלית שממנה יכולה המכונית לרדת ללא נזק. זוויות גישה וגישה נקראות גם זוויות רמפה .
שביתה וטבילה: שביתה וטבילה מתייחסים לכיוון או גישה של תכונה גיאולוגית. קו המכה של מיטה, תקלה או תכונה מישורית אחרת, הוא קו המייצג את הצומת של אותה תכונה עם מישור אופקי. על גבי מפה גיאולוגית, זה מיוצג עם קטע קו ישר קצר המכוון במקביל לקו המכה. ניתן לתת שביתה כמצפן רביעי הנושא את קו השביתה או במונחים של מזרח או מערב של צפון אמיתי או דרום, מספר תלת ספרתי יחיד המייצג את האזימוט, שם המספר התחתון בדרך כלל ניתן, או את מספר האזימוט ואחריו סימן התואר.
מערכת קואורדינטות כדורית: במתמטיקה, מערכת קואורדינטות כדורית היא מערכת קואורדינטות לחלל תלת מימדי שבו מיקום הנקודה מוגדר על ידי שלושה מספרים: המרחק הרדיאלי של אותה נקודה ממקור קבוע, זווית הקוטב שלה נמדדת מכיוון שיא קבוע, ו הזווית האזימוטלית של השלכתו האורתוגונלית במישור התייחסות העוברת דרך המקור והיא אורתוגונלית לזנית, נמדדת מכיוון ייחוס קבוע במישור זה. ניתן לראות בו את הגרסה התלת מימדית של מערכת הקואורדינטות הקוטביות.
זווית הכניסה: Angle of Entry הוא אלבום אקוסטי חי בהיקף מוגבל שהוקלט על ידי ציפורני הבשר במהלך הופעתם של Envy of Angels בבריטניה בשנת 1997 ושוחרר בלייבל המנהלים שלהם. הוא נמכר בהופעות ובאינטרנט.
חיכוך: חיכוך הוא הכוח העומד בפני תנועה יחסית של משטחים מוצקים, שכבות נוזליות ואלמנטים חומריים הגולשים זה כנגד זה. ישנם מספר סוגים של חיכוכים: חיכוך יבש הוא כוח המתנגד לתנועה רוחבית יחסית של שני משטחים מוצקים במגע. חיכוך יבש מחולק לחיכוך סטטי (" חיכוך ") בין משטחים שאינם נעים, וחיכוך קינטי בין משטחים נעים. למעט חיכוך אטומי או מולקולרי, חיכוך יבש נובע בדרך כלל מאינטראקציה בין תכונות פני השטח, המכונות אספרציות. חיכוך נוזלי מתאר את החיכוך בין שכבות של נוזל צמיג שנע ביחס זה לזה. חיכוך משומן הוא מקרה של חיכוך נוזלי בו נוזל חומר סיכה מפריד בין שני משטחים מוצקים. חיכוך העור הוא מרכיב של גרירה, הכוח העמיד בפני תנועת נוזל על פני גוף הגוף. חיכוך פנימי הוא הכוח העמיד בפני תנועה בין היסודות המרכיבים חומר מוצק בזמן שהוא עובר דפורמציה.
זָוִית פְּגִיעָה: זווית ההיארעות היא מדד לסטייה של משהו מ"ישר ", והיא עשויה להתייחס ל: זווית הפגיעה (אווירודינמיקה), זווית בין אקורד כנף לציר האורך, להבדיל מזווית ההתקפה, שהיא יחסית לזרימת האוויר. זווית ההיארעות (אופטיקה), המתארת ​​את התקרבות הקרן למשטח
זווית ההיארעות (אווירודינמיקה): במטוסים בעלי כנף קבועה, זווית הכניסה היא הזווית בין קו האקורד של הכנף שבו הכנף מותקנת על גוף המטוס, לבין ציר ייחוס לאורך גוף המטוס. זווית הכניסה קבועה בתכנון המטוס, ולמעט יוצאים מן הכלל, לא ניתנת לגיוון בטיסה.
זווית ההיארעות (אווירודינמיקה): במטוסים בעלי כנף קבועה, זווית הכניסה היא הזווית בין קו האקורד של הכנף שבו הכנף מותקנת על גוף המטוס, לבין ציר ייחוס לאורך גוף המטוס. זווית הכניסה קבועה בתכנון המטוס, ולמעט יוצאים מן הכלל, לא ניתנת לגיוון בטיסה.
זָוִית פְּגִיעָה: זווית ההיארעות היא מדד לסטייה של משהו מ"ישר ", והיא עשויה להתייחס ל: זווית הפגיעה (אווירודינמיקה), זווית בין אקורד כנף לציר האורך, להבדיל מזווית ההתקפה, שהיא יחסית לזרימת האוויר. זווית ההיארעות (אופטיקה), המתארת ​​את התקרבות הקרן למשטח
זווית ההיארעות (אופטיקה): באופטיקה גיאומטרית זווית ההיארעות היא הזווית שבין קרן המתרחשת על פני השטח לקו המאונך לפני השטח בנקודת השכיחות, הנקראת נורמלי. הקרן יכולה להיווצר על ידי כל גל: אופטי, אקוסטי, מיקרוגל, רנטגן וכן הלאה. באיור למטה, הקו המייצג קרן עושה זווית θ עם הנורמלי. זווית הזרימה בה האור מוחזר לראשונה באופן מוחלט מכונה הזווית הקריטית. זווית ההשתקפות וזווית השבירה הן זוויות אחרות הקשורות לקורות.
זווית הרשימה: זווית הרשימה היא המידה בה כלי שיט מתנשא ליציאה או למוטון בשיווי משקל - ללא כוחות חיצוניים הפועלים עליו.
זווית שומן: זווית שוויון היא מצבה של ספינה שאינה יציבה כאשר היא זקופה ולכן תופסת זווית של עקב ליציאה או למוט.
זווית פנימית: הזווית בחזה היא המפרק הסינארטרוטי שנוצר על ידי המפרק של המנוברום וגוף עצם החזה.
זווית לחץ: זווית הלחץ ביחס לשיני גלגל השיניים, המכונה גם זווית העקיפה , היא הזווית שבין פני השן לבין משיק גלגל ההילוכים. ליתר דיוק הזווית בנקודת גובה בין קו הלחץ למישור המשיק למשטח המגרש. זווית הלחץ נותנת את הכיוון הנורמלי לפרופיל השן. זווית הלחץ שווה לזווית הפרופיל במעגל המגרש הסטנדרטי וניתן לכנותה זווית הלחץ "הסטנדרטית" באותה נקודה. הערכים הסטנדרטיים הם 14.5 ו -20 מעלות. הילוכים קודמים עם זווית לחץ 14.5 שימשו בדרך כלל מכיוון שהקוסינוס גדול יותר לזווית קטנה יותר, ומספק יותר העברת כוח ופחות לחץ על המסב; עם זאת, שיניים עם זוויות לחץ קטנות יותר חלשות יותר. כדי להפעיל הילוכים בצורה תקינה יש להתאים את זוויות הלחץ שלהם.
זווית ההקבלה: בגיאומטריה היפרבולית, זווית ההקבלה , היא הזווית בקודקוד הזווית הלא נכון של משולש היפרבולי ימני בעל שני צלעות מקבילות אסימפטוטיות. הזווית תלויה באורך הקטע a בין הזווית הנכונה לקודקוד זווית ההקבלה.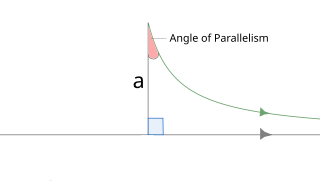
זווית דו-כיוונית: זווית דו- כיוונית היא הזווית בין שני מישורים מצטלבים או חצי מישורים. בכימיה זו הזווית עם כיוון השעון בין חצי מישור דרך שני קבוצות של שלושה אטומים, שיש להם שני אטומים משותפים. בגיאומטריה מוצקה, הוא מוגדר כאיחוד של קו ושני מישורי חצי שקו זה כקצה משותף. בממדים גבוהים יותר, זווית דו-כיוונית מייצגת את הזווית בין שני מישורים-יתר. מראים כי מישורים של מכונה מעופפת נמצאים בזווית דו-כיוונית חיובית כאשר מישור הראשי של הימני והמטה נוטה כלפי מעלה לציר הרוחב. כאשר נוטים כלפי מטה, נאמר שהם נמצאים בזווית דיאדרלית שלילית.
זווית לחץ: זווית הלחץ ביחס לשיני גלגל השיניים, המכונה גם זווית העקיפה , היא הזווית שבין פני השן לבין משיק גלגל ההילוכים. ליתר דיוק הזווית בנקודת גובה בין קו הלחץ למישור המשיק למשטח המגרש. זווית הלחץ נותנת את הכיוון הנורמלי לפרופיל השן. זווית הלחץ שווה לזווית הפרופיל במעגל המגרש הסטנדרטי וניתן לכנותה זווית הלחץ "הסטנדרטית" באותה נקודה. הערכים הסטנדרטיים הם 14.5 ו -20 מעלות. הילוכים קודמים עם זווית לחץ 14.5 שימשו בדרך כלל מכיוון שהקוסינוס גדול יותר לזווית קטנה יותר, ומספק יותר העברת כוח ופחות לחץ על המסב; עם זאת, שיניים עם זוויות לחץ קטנות יותר חלשות יותר. כדי להפעיל הילוכים בצורה תקינה יש להתאים את זוויות הלחץ שלהם.
השתקפות (פיזיקה): השתקפות היא שינוי כיוון חזית הגל בממשק בין שני מדיות שונות כך שחזית הגל חוזרת למדיום שממנו מקורו. דוגמאות נפוצות כוללות השתקפות גלי אור, קול ומים. חוק ההשתקפות אומר כי לצורך השתקפות ספקולרית הזווית בה הגל נופל על פני השטח שווה לזווית בה הוא משתקף. מראות מציגות השתקפות ספקולרית.
החוק של סנל: החוק של סנל הוא נוסחה המשמשת לתיאור הקשר בין זוויות השכיחות והשבירה, כאשר מתייחסים לאור או לגלים אחרים העוברים דרך גבול בין שני מדיות איזוטרופיות שונות, כגון מים, זכוכית או אוויר.
זווית המנוחה: זווית המנוחה , או זווית המנוחה הקריטית , של חומר גרגירי היא הזווית התלולה ביותר של ירידה או טבילה ביחס למישור האופקי שאליו ניתן לערום חומר מבלי לרדת. בזווית זו, החומר על פני השיפוע נמצא על סף החלקה. זווית המנוחה יכולה לנוע בין 0 ° ל -90 °. המורפולוגיה של החומר משפיעה על זווית המנוחה; לא ניתן לערום גרגרי חול חלקים ומעוגלים בצורה תלולה כמו חולות מחוספסים ומשולבים זה בזה. זווית המנוחה יכולה להיות מושפעת גם מתוספות ממסים. אם כמות קטנה של מים מסוגלת לגשר על הפערים בין חלקיקים, משיכה אלקטרוסטטית של המים למשטחים מינרליים תגדיל את זווית המנוחה, וכמויות נלוות כגון חוזק האדמה.
בית החזה: כלוב הצלעות הוא סידור הצלעות המחוברות לעמוד החוליה ולחזה בבית החזה של מרבית החוליות הסוגר ומגן על האיברים החיוניים כמו הלב, הריאות והכלים הגדולים.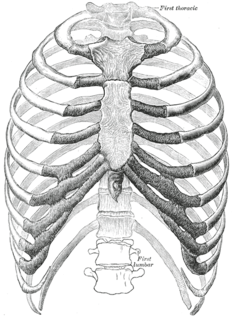
זווית סיבוב: במתמטיקה, זווית הסיבוב היא מדידה של הכמות, כלומר זווית, שדמות מסובבת סביב נקודה קבועה, לעתים קרובות מרכז המעגל. סיבוב בכיוון השעון נחשב לסיבוב שלילי, כך, למשל, סיבוב של 310 ° (נגד כיוון השעון) יכול להיקרא גם סיבוב של –50 °. סיבוב נגד כיוון השעון של יותר מפנייה שלמה אחת נמדד בדרך כלל מודולו 360 °, כלומר 360 ° מופחתים כמה שיותר פעמים כדי להשאיר מדידה לא שלילית פחות מ -360 °.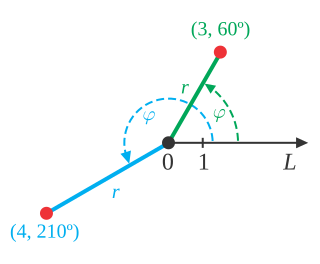
עֶצֶם הַשֶׁכֶם: באנטומיה, עצם השכמה , המכונה גם עצם הכתף , הכתף , עצם הכנף או עצם הלהב , היא העצם המחברת את עצם הזרוע עם עצם הבריח. כמו עצמותיהם המחוברות, עצמות השכמות מזווגות, כאשר כל עצם השכמה משני צדי הגוף מהווה בערך תמונת מראה של השנייה. השם נובע מהמילה הלטינית הקלאסית עבור כף או חפירה קטנה, שנחשבה דומה לה.
זווית החלקה: בדינמיקה של הרכב, זווית החלקה או זווית החלקה צדדית היא הזווית שבין כיוון הגלגל לכיוון לכיוון בו הוא באמת נוסע. זווית החלקה זו גורמת לכוח, כוח הפנייה, שנמצא במישור טלאי המגע ומאונך לצומת טלאי המגע ובין אמצע הגלגל. כוח הפניה הזה גדל באופן ליניארי בערך בזוויות החלקה הראשונות, ואז גדל באופן לא ליניארי למקסימום לפני שהוא מתחיל לרדת.